Phần tự luận SVIP

Hướng dẫn giải:

a. Ta có: $k=\dfrac{y}{x}=\dfrac{-4}{5}$;

b. Biểu diễn $y$ theo $x: y=\dfrac{-4}{5} x$;

c. Khi $x=-10$ thì $y=\dfrac{-4}{5} x=\dfrac{-4}{5} .(-10)=8$
Khi $x=2$ thì $y=\dfrac{-4}{5} .x=\dfrac{-4}{5} .2=\dfrac{-8}{5}$.

Hướng dẫn giải:

a) Gọi a, b, c lần lượt là số đo của ba góc ${A},  {B},  {C}, ( {a},  {b},  {c} \in \mathbb{N}^*$ đơn vị:$ ^{\circ})$. Vì số đo các góc $A, B, C$ lần lượt tỉ lệ với các số $2 ; 4 ; 6$. nên:

$\dfrac{a}{2}=\dfrac{b}{4}=\dfrac{c}{6}$ và ${a}+ {b}+ {c}=180^{\circ}$

Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:

$\dfrac{a}{2}=\dfrac{b}{4}=\dfrac{c}{6}=\dfrac{a+b+c}{2+4+6}=\dfrac{180}{12}=15^{\circ}$

Suy ra:

$\dfrac{a}{2}=15^{\circ} \Rightarrow a=30^{\circ} ; \dfrac{b}{4}=15^{\circ} \Rightarrow b=60^{\circ} ; \dfrac{c}{6}=15^{\circ} \Rightarrow c=90^{\circ}$ (thỏa mãn)

Vậy số đo của ba góc $A, B, C$ lần lượt là $30^{\circ}; 60^{\circ}; 90^{\circ}$.

b) Vì $\widehat{A}<\widehat{B}<\widehat{C}$  nên ${BC}< {AC}< {AB}$.

Hướng dẫn giải:

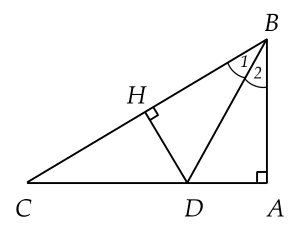
a) ${BA}< {BC}$ ( Quan hệ đường vuông góc và đường xiên)

b)Xét hai tam giác vuông ${ABD}$ và ${HBD}$, ta có:

$\widehat{B A D}=\widehat{B H D}=90^{\circ}$

$\widehat{B_1}=\widehat{B_2}$ (vì $BD$ là tia phân giác của góc $ABC$).

Cạnh huyền $BD$ chung.

Suy ra $\Delta ABD = \Delta HBD$ (cạnh huyền, góc nhọn).

Suy ra $AD = HD$ (2 cạnh tương ứng) (1).

c) Trong tam giác vuông $ {DHC}$ có $ \widehat{DHC}=90^{\circ}$. Suy ra $  {DH}< {DC}$ (cạnh góc vuông nhỏ hơn cạnh huyền) (2).

Từ (1) và (2) suy ra: $ {AD}< {DC}$.

Hướng dẫn giải:

Gọi số công nhân tham gia làm việc của đội thứ nhất, đội thứ hai, đội thứ ba lần lượt là $ {x},  {y},  {z}$ $(x,y,z \in \mathbb{N}^*,$ đơn vị: người $)$.

Số công nhân của đội thứ ba ít hơn số công nhân của đội thứ hai là $5$ người nên ${y}- {z}=5.$

Với cùng một khối lượng công việc, số công nhân tham gia làm việc và thời gian hoàn thành công việc của mỗi đội là hai đại lượng tỉ lệ nghịch với nhau.

Do đó, ta có $2 x=3 y=4 z$, hay $\dfrac{x}{\dfrac{1}{2}}=\dfrac{y}{\dfrac{1}{3}}=\dfrac{z}{\dfrac{1}{4}}$.

Áp dụng tính chất của dãy tỉ số bằng nhau tính $ {x},  {y},  {z}$, ta có:

$\dfrac{x}{\dfrac{1}{2}}=\dfrac{y}{\dfrac{1}{3}}=\dfrac{z}{\dfrac{1}{4}}= \dfrac{y-z}{\dfrac{1}{3} - \dfrac{1}{4}} = \dfrac{5}{\dfrac{1}{12}}=60$.

Vậy $x=30;y=20;z=15$ (người).

Kết luận: số công nhân tham gia làm việc của đội thứ nhất, đội thứ hai, đội thứ ba lần lượt là $30$ người, $20$ người, $15$ người.