olm
Đăng nhập Đăng ký Trợ giúp

Bài học cùng chủ đề

Báo cáo học liệu
Mua học liệu
Mua học liệu:
  • Số dư ví của bạn: 0 coin - 0 Xu
  • Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Thông tin của bạn

Đề thi đánh giá năng lực - đề số 1 SVIP

In bài

Yêu cầu đăng nhập!

Bạn chưa đăng nhập. Hãy đăng nhập để làm bài thi tại đây!

Câu 1 (1đ):

Cho phương trình bậc hai ax2+bx+c=0a{{x}^{2}}+bx+c=0, (a≠0)\left( a\ne 0 \right). Điều kiện để phương trình có nghiệm là

b2−4ac>0.{{b}^{2}}-4ac>0.
b2−4ac≥0.{{b}^{2}}-4ac\ge 0.
b2−ac≥0{{b}^{2}}-ac\ge 0.
b2+4ac≥0.{{b}^{2}}+4ac\ge 0.
Câu 2 (1đ):

Gọi x1, x2{{x}_{1}}, \, {{x}_{2}} là hai nghiệm của phương trình 5x2−3x−1=05{{x}^{2}}-3x-1=0. Khẳng định nào sau đây đúng?

x1x2=−35.{{x}_{1}}{{x}_{2}}=-\dfrac{3}{5}.
x1x2=15.{{x}_{1}}{{x}_{2}}=\dfrac{1}{5}.
x1+x2=−35.{{x}_{1}}+{{x}_{2}}=-\dfrac{3}{5}.
x1+x2=35.{{x}_{1}}+{{x}_{2}}=\dfrac{3}{5}.
Câu 3 (1đ):

Hệ phương trình nào sau đây vô nghiệm?

{2x−3y=1−10x=5\left\{ \begin{aligned} & 2x-3y=1 \\ & -10x=5 \\\end{aligned} \right..
{2x−3y=115x=5\left\{ \begin{aligned} & 2x-3y=1 \\ & 15x=5 \\ \end{aligned} \right..
{2x−3y=1−2x+3y=−1\left\{ \begin{aligned} & 2x-3y=1 \\ & -2x+3y=-1 \\ \end{aligned} \right..
{2x−3y=1−10x+15y=5\left\{ \begin{aligned}& 2x-3y=1 \\& -10x+15y=5 \\ \end{aligned} \right..
Câu 4 (1đ):

Phương trình nào dưới đây vô nghiệm?

−x−1=5.\sqrt{-x-1}=5.
x−x−1=0.x\sqrt{-x-1}=0.
2x+1=0.\sqrt{2x+1}=0.
−x−1=−2.\sqrt{-x-1}=-2.
Câu 5 (1đ):

Điểm có tọa độ nào sau đây không nằm trên đồ thị hàm số y=−2x2y=-2x^2?

(−3;−6).\left( -\sqrt{3};-6 \right).
(1;−2).\left( 1;-2 \right).
(3;6).\left( \sqrt{3};6 \right).
(5;−50).\left( 5;-50 \right).
Câu 6 (1đ):

Bánh xe của một ròng rọc có chu vi bằng 540 mm. Dây cua roa bao bánh xe theo cung AB có độ dài 200 mm (hình vẽ).

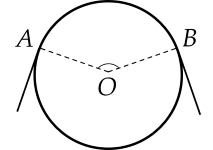
loading...

Tính (chính xác đến phút) số đo AOB^\widehat{AOB}.

123∘^{\circ}20'.
133∘^{\circ}20'.
133∘^{\circ}10'.
103∘^{\circ}10'.
Câu 7 (1đ):

Người ta nhấn chìm hoàn toàn một vật vào lọ thủy tinh có nước dạng hình trụ. Diện tích đáy của lọ thủy tinh bằng 12,812,8 cm2^2, nước trong lọ dâng cao thêm 8,58,5 mm. Vật nặng đó có thể tích bằng bao nhiêu cm3^3?

10,1210,12 cm3^3.
10,8810,88 cm3^3.
9,889,88 cm3^3.
10,0810,08 cm3^3.
Câu 8 (1đ):

Thể tích hình nón với bán kính đáy rr và chiều cao hh được tính theo công thức nào dưới đây?

V=13πr2h.V=\dfrac{1}{3}\pi {{r}^{2}}h.
V=πr2h.V=\pi {{r}^{2}}h.
V=13πrh.V=\dfrac{1}{3}\pi rh.
V=3πr2h.V=3\pi {{r}^{2}}h.
Câu 9 (1đ):

Cho tam giác ABCABC có AB=6, AC=8, BC=10AB=6, \, AC=8, \, BC=10 (cm). Đường tròn ngoại tiếp tam giác ABCABC có diện tích bằng bao nhiêu cm2^2?

2525 (cm2^2).
25π25\pi (cm2^2).
1010 (cm2^2).
10π10\pi (cm2^2).
Câu 10 (1đ):

Cho biết chiều ngang khung thành bóng đá là 7,327,32 m. Hãy tính "góc sút" của quả phạt đền 1111 mét (làm tròn kết quả đến độ).

18∘18^{\circ}.
20∘20^{\circ}.
28∘28^{\circ}.
14∘14^{\circ}.
Câu 11 (1đ):

Tính giá trị biểu thức 3+22−2.\sqrt{3+2\sqrt{2}}-\sqrt{2}.

−1.-1.
1.1.
3+2.\sqrt{3+\sqrt{2}}.
2.\sqrt{2}.
Câu 12 (1đ):

Một khối Rubik có thể tích 512512 cm3^3. Độ dài cạnh của khối Rubik này bằng

1212 cm.
99 cm.
88 cm.
1111 cm.
Câu 13 (1đ):

Đọc đoạn văn bản dưới đây rồi trả lời các câu hỏi từ câu 13 đến câu 16.

Trái Đất và Vệ tinh nhân tạo

Trái Đất có dạng gần như là hình cầu với bán kính khoảng 66 400400 ki-lô-mét và là nơi sinh sống của loài người. Vệ tinh nhân tạo là những vật thể do con người chế tạo bay quanh một vật thể khác (hình 1).

loading... loading...
(hình 1) (hình 2)

Người đầu tiên nghĩ ra vệ tinh nhân tạo dùng cho truyền thông là nhà viết truyện khoa học giả tưởng Arthur C.Clarke vào năm 1945. Tuy nhiên vệ tinh nhân tạo đầu tiên là Sputnik 1 được Liên Xô phóng lên quỹ đạo ngày 4/10/1957. Một vệ tinh địa tĩnh chuyển động theo quỹ đạo tròn cách bề mặt Trái Đất khoảng 3636 000000 km, tâm quỹ đạo trùng với tâm Trái Đất (hình 2). Vệ tinh phát tín hiệu vô tuyến theo đường thẳng đến một số vị trí trên bề mặt Trái Đất.

Câu 1:

loading...

Trong hình trên, đường tròn tâm OO minh họa hình ảnh bề mặt trái đất; CC là vị trí của vệ tinh trong không gian. CEC E và CFC F là hai tiếp tuyến với đường tròn, các tiếp điểm là các vị trí xa nhất trên bề mặt trái đất có thể nhận được tín hiệu từ vệ tinh. Những điểm nào dưới đây là vị trí các điểm trên bề mặt Trái Đất nhận được sóng của vệ tinh?

CC.
OO.
EE.
FF.
DD.
Câu 2:

Trong thực tế, khoảng cách từ điểm CC đến điểm DD bằng km.

Câu 3:

Kí hiệu các khoảng cách CDCD, DODO và CECE theo thứ tự là hh, RR, dd. Công thức nào dưới đây đúng?

d=h2+Rhd=\sqrt{h^2+R h}.
d=h2+2Rhd=\sqrt{h^2+2 R h}.
d=h2−2Rhd=\sqrt{h^2-2 R h}.
d=h2+2Rhd=h^2+2 R h.
Câu 4:

Vị trí xa nhất trên bề mặt Trái Đất có thể nhận được tín hiệu từ vệ tính cách vệ tinh bao nhiêu ki-lô-mét? (làm tròn kết quả đến hàng đơn vị)

Đáp án: km.

Câu 14 (1đ):

Đọc đoạn văn bản dưới đây rồi trả lời hai câu hỏi 17 và 18.

loading...

Sóng thần (hình vẽ) là một loạt các đợt sóng tạo nên khi một thể tích lớn nước của đại dương chuyển dịch chớp nhoáng trên một quy mô lớn. Động đất cùng những dịch chuyển địa chất lớn bên trên hoặc bên dưới mặt nước đều có thể gây ra sóng thần. Các cơn sóng thần thường xuất phát từ đáy đại dương và rất xa bờ. Kkhi còn ở ngoài khơi xa, sóng có biên độ (chiều cao của sóng) tuy khá nhỏ nhưng lại có chiều dài tới hàng trăm ki-lô-mét. Chúng vượt qua đại dương với tốc độ khủng khiếp tới 500500 dặm một giờ. Khi tiến sát đất liền, đáy biển nông, sóng không còn dịch chuyển nhanh được nữa và nó dựng đứng lên, có chiều cao bằng một tòa nhà cao tầng và có sức tàn phá khủng khiếp. Tốc độ của sóng thần liên quan chặt chẽ với độ sâu của đại dương bởi công thức vs=dgv_s=\sqrt{d g}, trong đó vsv_s là vận tốc của sóng thần, g≈9,81g\approx 9,81 m/s2^2 là gia tốc rơi tự do và là độ sâu đại dương tính bằng mét.

Câu 1:

Ước tính vận tốc của các con sóng xuất phát từ độ sâu 33 790790 m là bao nhiêu km/h?

694694 km/h.
649649 km/h.
659659 km/h.
695695 km/h.
Câu 2:

Susan Kieffer, một chuyên gia cơ học chất lỏng địa chất của đại học Illinois (Mỹ), đã nghiên cứu năng lượng của trận sóng thần Tohuku 2011 ở Nhật Bản. Các tính toán của Kieffer cho thấy sóng thần Tohuku đạt vận tốc trung bình khoảng 220220 m/s. Hãy tính độ sâu của đại dương nơi sóng thần Tohuku xuất phát (làm tròn các kết quả đến hàng đơn vị).

Đáp án: m.

Câu 15 (1đ):

Đọc đoạn văn bản dưới đây rồi trả lời hai câu hỏi 19 và 20.

Theo thống kê của Tổng cục Thống kê, dân số của một thành phố sau 22 năm đã tăng từ 22 (triệu người) lên 2,0482882,048288 (triệu người).

Câu 1:

Gọi số phần trăm dân số thành phố sau hai năm đã tăng tăng trung bình trong hai năm đó là xx (%). Viết biểu thức tính theo dân số thành phố đó sau 11 năm.

x+2x+2 triệu.
2x+12x+1 triệu.
2(x+1)2(x+1) triệu.
2(x+2)2(x+2) triệu.
Câu 2:

Viết biểu thức tính theo dân số thành phố đó sau 22 năm. Trong 22 năm đó, hàng năm dân số thành phố tăng trung bình bao nhiêu phần trăm?

2,2%2,2 \%.
1,2%1,2 \%.
0,2%0,2 \%.
2,1%2,1 \%.
OLM©2022OLM \copyright 2022
Truy vết IP log
Báo lỗi câu hỏi
Bạn đã gặp lỗi gì ở câu hỏi này, hãy mô tả vào ô bên dưới. Với mỗi lỗi thông báo đúng, OLM sẽ tặng bạn 1-3 ngày VIP!
Bạn có thể báo lỗi bằng hình ảnh tại đây!!!
Các khóa học có thể bạn quan tâm
Tổng thanh toán: 0đ (Tiết kiệm: 0đ)
Tới giỏ hàng
Yêu cầu VIP