Rút gọn biểu thức $\sqrt{a^4.(2a-1)^2}$ với $a\ge \dfrac{1}{2}$ ta được

Cho $m$ bất kỳ, khẳng định nào dưới đây đúng?

Cặp số $(3;-5)$ là nghiệm của hệ phương trình nào sau đây?

Một ô tô dự định đi từ $A$ đến $B$ trong một thời gian nhất định. Nếu xe chạy mỗi giờ nhanh hơn $10$ km thì đến nơi sớm hơn dự định $3$ giờ, còn nếu xe chạy chậm lại mỗi giờ $10$ km thì đến nơi chậm mất $5$ giờ. Vận tốc của xe lúc ban đầu là

Kết quả bài thi $200$ câu trắc nghiệm tiếng anh trên Internet của $80$ học sinh với thang điểm $2\,000$ được ghi lại như sau:

Có $3$ học sinh được $880$ điểm; $24$ học sinh được $1\,450$ điểm; $30$ học sinh được $$ điểm; $21$ học sinh được $1\,800$ điểm; còn lại là số học sinh được $2\,000$ điểm.

Tần số tương đối của học sinh đạt được $2\,000$ điểm là

Cho tam giác $ABC$ vuông tại $A$ có $BC=8$ cm, $AC = 6$ cm. Tỉ số lượng giác của $\tan C$ (làm tròn đến chữ số thập phân thứ 2) là

Cho hình trụ có bán kính đáy $R = 4$ (cm) và chiều cao $h=5$ (cm). Diện tích xung quanh của hình trụ là

Cho tứ giác $MNPQ$ nội tiếp đường tròn với $\widehat{MQP}-\widehat{MNP}=10^\circ$. Số đo $\widehat{MQP}$ bằng

Giải phương trình: $5x^2 - 3x - 2$.

Giải hệ phương trình: $\left\{ \begin{aligned} & x+2y=-1 \\ & 2x-5y=7 \end{aligned} \right.$.

Trong cuộc thi “Đố vui để học”, mỗi thí sinh phải trả lời $12$ câu hỏi của ban tổ chức. Mỗi câu hỏi gồm bốn phương án, trong đó chỉ có một phương án đúng. Với mỗi câu hỏi, nếu trả lời đúng thì được cộng $5$ điểm, trả lời sai bị trừ $2$ điểm. Khi bắt đầu cuộc thi, mỗi thí sinh có sẵn $20$ điểm. Thí sinh nào đạt từ $50$ điểm trở lên sẽ được vào vòng thi tiếp theo. Hỏi thí sinh phải trả lời đúng ít nhất bao nhiêu câu thì được vào vòng thi tiếp theo?

Tấm bìa cứng $A$ hình tròn được chia thành 3 hình quạt có diện tích bằng nhau, đánh số $1$; $2$; $3$ và tấm bìa cứng B hình tròn được chia thành 5 hình quạt có diện tích bằng nhau, đánh số $1$; $2$; $3$; $4$; $5$ (xem hình vẽ). Trục quay của $A$ và $B$ được gắn mũi tên ở tâm. Bạn Bình quay tấm bìa $A$, bạn An quay tấm bìa $B$. Quan sát xem mũi tên dừng ở hình quạt nào trên hai tấm bìa.

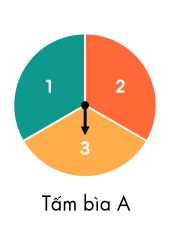
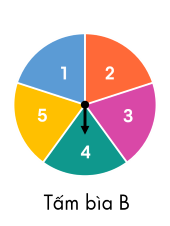
Tính xác suất của các biến cố sau:

$T$: “Tích hai số ở hình quạt mà hai mũi tên chỉ vào bằng $6$”;

$M$: “Tích hai số ở hình quạt mà hai mũi tên chỉ vào nhỏ hơn $5$”;

$L$: “Tích hai số ở hình quạt mà hai mũi tên chỉ vào là số chẵn”.

Cho phương trình: $2x^2 - 4x - 1 = 0$ có $2$ nghiệm là $x_1;\, x_2$. Không giải phương trình, hãy tính giá trị của biểu thức: $T=\dfrac{x_1}{x_2}+\dfrac{5}{2} (x_1-x_2)^2+\dfrac{x_2}{x_1}$.

Một hợp kim gồm sắt và carbon trong đó có $5$ g carbon. Nếu thêm 15g carbon nữa vào hợp kim này ta được hợp kim mới mà trong đó lượng sắt đã giảm đi $30\%$ so với ban đầu. Biết rằng trong hợp kim ban đầu khối lượng sắt nhiều hơn carbon. Tính khối lượng ban đầu của hợp kim.

Cho biểu thức $P=\Big( \dfrac{x-4}{x-3\sqrt{x}+2}+1 \Big):\dfrac{1}{2x-3\sqrt{x}+1}$. Với $x \ge 5$, tìm giá trị nhỏ nhất của $T = P + \dfrac{10}{x}$.

Một lọ nước hoa có hình dạng bên ngoài là hình cầu làm bằng thuỷ tinh có đường kính $8$ cm. Lòng bên trong của lọ cũng là một hình cầu nhỏ cùng tâm với hình cầu bên ngoài để chứa nước hoa. Hỏi phải làm lọ nước hoa có độ dày thành lọ là bao nhiêu cm để chứa được lượng nước hoa bên trong là $120$ ml? (làm tròn đến hàng phần mười). Biết rằng lượng nước hoa được chứa trong lọ chiếm $80\%$ thể tích của phần có thể chứa nước hoa.

Cho đường tròn $(O; R)$. Từ một điểm $M$ nằm ngoài đường tròn tâm, kẻ hai tiếp tuyến $MA$, $MB$ đến $(O)$ (với $A$, $B$ là các tiếp điểm). Qua $A$ kẻ đường thẳng song song với $MO$ cắt đường tròn tại $E$ đường thẳng $MF$ cắt đường tròn tại $F$ đường thẳng $AF$ cắt $MO$ tại $N$.

a) Chứng minh tứ giác $MAOB$ nội tiếp đường tròn.

b) Chứng minh $MN^2 = NF.NA$.

c) Gọi $H$ là giao điểm của $MO$ và $AB$. Chứng minh $MN = NH$ và $\dfrac{HB^2}{HF^2} - \dfrac{EF}{MF} = 1$.