Bài học cùng chủ đề
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Đề số 2 (Phần tự luận 7 điểm) SVIP
Thực hiện phép tính (Tính hợp lý nếu có thể).
a) $\dfrac{11}{24}-\dfrac{5}{41}+\dfrac{13}{24}+0,5-\dfrac{36}{41}$.
b) $\dfrac{1}{2} \cdot \dfrac{3}{4}+\dfrac{1}{2} \cdot \dfrac{1}{4}+\dfrac{1}{2}$.
c) $\Big(\dfrac{-3}{4}\Big)^2:\Big(\dfrac{-1}{4}\Big)^2+9 \cdot\Big(\dfrac{-1}{9}\Big)+\Big( \dfrac{-3}{2} \Big)$.
d) $\sqrt{0,25} \cdot(-3)^3-\sqrt{\dfrac{1}{81}}:\Big(\dfrac{-1}{3}\Big)^3$.
Hướng dẫn giải:
a) $\dfrac{11}{24}-\dfrac{5}{41}+\dfrac{13}{24}+0,5-\dfrac{36}{41}=\Big(\dfrac{11}{24}+\dfrac{13}{24}\Big)-\Big(\dfrac{5}{41}+\dfrac{36}{41}\Big)+0,5=1-1+0,5=0,5$.
b) $\dfrac{1}{2} \cdot \dfrac{3}{4}+\dfrac{1}{2} \cdot \dfrac{1}{4}+\dfrac{1}{2}=\dfrac{1}{2} \cdot\Big(\dfrac{3}{4}+\dfrac{1}{4}+1\Big)=\dfrac{1}{2} \cdot 2=1$.
c) $\Big(\dfrac{-3}{4}\Big)^2:\Big(\dfrac{-1}{4}\Big)^2+9 \cdot\Big(\dfrac{-1}{9}\Big)+\Big(\dfrac{-3}{2}\Big)=\dfrac{9}{16}: \dfrac{1}{16}-1-\dfrac{3}{2}=9-1-\dfrac{3}{2}=\dfrac{13}{2}.$
d) $\sqrt{0,25} \cdot(-3)^3-\sqrt{\dfrac{1}{81}}:\Big(\dfrac{-1}{3}\Big)^3=0,5 \cdot(-27)-\dfrac{1}{9}: \dfrac{-1}{27}=\dfrac{-27}{2}+3=\dfrac{-21}{2}$.
Tìm số hữu tỉ $x$, biết
a) $x-\dfrac{2}{3}=\dfrac{1}{6}$;
b) $2 x+\dfrac{1}{2}=-\dfrac{5}{3}$;
c) $3 x+\dfrac{3}{2}=x-\dfrac{5}{3}$.
Hướng dẫn giải:
a) $x-\dfrac{2}{3}=\dfrac{1}{6}$
$x=\dfrac{1}{6}+\dfrac{2}{3}$
$x=\dfrac{1}{6}+\dfrac{4}{6}$
$x=\dfrac{5}{6}$.
b) $2 x+\dfrac{1}{2}=-\dfrac{5}{3}$
$2 x=-\dfrac{5}{3}-\dfrac{1}{2}$
$2 x=-\dfrac{13}{6}$
$x=-\dfrac{13}{12}$.
c) $3 x+\dfrac{3}{2}=x-\dfrac{5}{3}$
$3 x-x=-\dfrac{5}{3} - \dfrac{3}{2}$
$2x=\dfrac{-19}{6}$
$x=\dfrac{-19}{12}$.
Cho hình vẽ biết $\widehat{ACB}=40^{\circ};$ $\widehat{BAC}=100^{\circ}$, $Ay$ là tia phân giác của $\widehat{CAx}$.
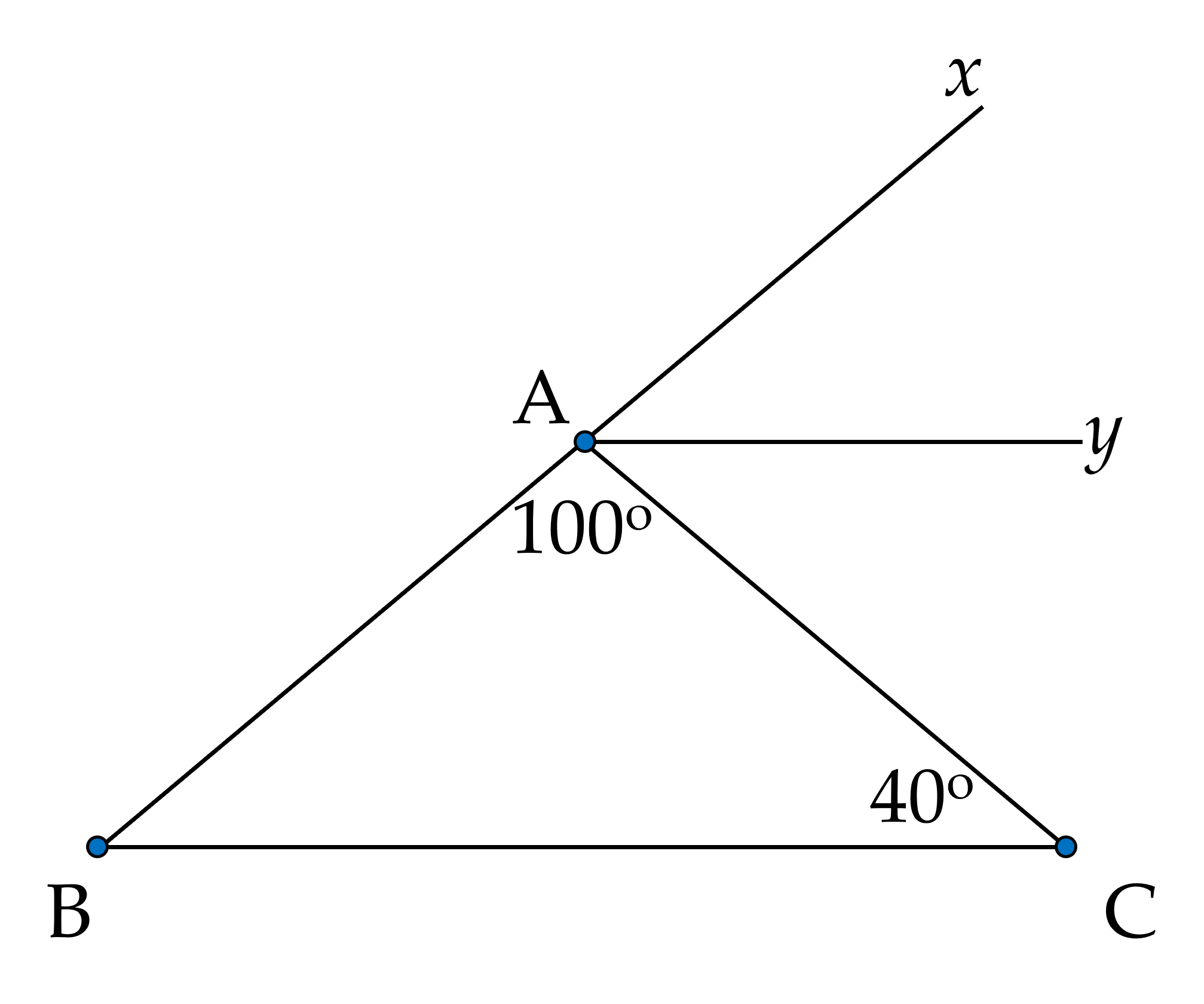
a) Tính $\widehat{CAx}$.
b) Chứng minh $Ay$ // $BC$.
c) Tính số đo $\widehat{ABC}$.
Hướng dẫn giải:
a) Ta có $\widehat{CAx}+\widehat{BAC}=180^{\circ}$ (hai góc kề bù).
Suy ra: $\widehat{CAx} = 180^{\circ} - \widehat{BAC}$
$\widehat{CAx} = 180^{\circ} - 100^{\circ}=80^{\circ}$.
b) Vì $Ay$ là tia phân giác của $\widehat{CAx}$, nên
$\widehat{CAy}=\widehat{xAy}=\dfrac{1}{2}.\widehat{CAx}=\dfrac{1}{2}.80^{\circ} = 40^{\circ}$.
Vậy $\widehat{CAy} = \widehat{ACB}$, mà hai góc này ở vị trí so le trong, do đó $Ay$ // $BC$.
c) Do $Ay$ // $BC$, nên $\widehat{xAy}=\widehat{ABC}$ (hai góc đồng vị).
Suy ra $\widehat{ABC}=40^{\circ}$.
Một cửa hàng sách có chương trình khuyến mãi như sau: Khách hàng có thẻ thành viên sẽ được giảm $10 \%$ tổng số tiền của hoá đơn. Bạn Lan có thẻ thành viên và bạn mua 3 quyển sách, mỗi quyển sách có giá $120$ $000$ đồng. Bạn đưa cho cô thu ngân $350$ $000$ đồng. Hỏi bạn Lan được trả lại bao nhiêu tiền?
Hướng dẫn giải:
Số tiền 3 quyển sách là:
$3.120\,000=360\,000$ (đồng)
Số tiền Lan phải trả khi có thẻ thành viên là:
$360\,000 .(100 \%-10 \%)=324\,000$ (đồng)
Ta có: $350\,000-324\,000=26\,000$ (đồng).
Do đó Lan được trả lại $26\,000$ đồng.
Cho biết $1^2+2^2+3^2+\ldots+10^2=385$.
Tính $A=3^2+6^2+9^2+\ldots+30^2$.
Hướng dẫn giải:
Ta có: $1^2+2^2+3^2+\ldots+10^2=385$
Suy ra: $\left(1^2+2^2+3^2+\ldots+10^2\right).3^2=385.3^2$
$(1.3)^2+(2.3)^2+(3.3)^2+\ldots+(10.3)^2=385.3^2$
Do đó $A=3^2+6^2+9^2+\ldots+30^2=3465$.
