Điểm đánh giá học kì I môn Toán của lớp 9A được người ta ghi lại bảng như sau:

Lập bảng tần số ghép nhóm và bảng tần số tương đối ghép nhóm cho mẫu số liệu trên với các nhóm $[5;6,5); \, [6,5;8); \, [8;9,5)$.

Lấy ngẫu nhiên một thẻ từ một hộp chứa $20$ thẻ cùng hình dạng, kích thước được đánh số từ $1$ đến $20$. Tìm xác suất để thẻ được lấy ghi số lẻ và chia hết cho $5$.

Cho hai biểu thức $M=\dfrac{\sqrt{x}-2}{\sqrt{x}+1}$ và $N=\dfrac{\sqrt{x}}{\sqrt{x}+1}-\dfrac{\sqrt{x}-4}{1-x}$ với $x\ge 0, \, x\ne 1$.

a) Tính giá trị của biểu thức $M$ khi $x=8+2\sqrt{7}$.

b) Biết $P=\dfrac{M}{N}$. Chứng minh $P=\dfrac{\sqrt{x}-1}{\sqrt{x}+2}$.

c) Tìm giá trị $x$ là số nguyên tố thoả mãn $P\le \dfrac{1}{2}$.

Hai trường THCS trên địa bàn một huyện có $400$ học sinh tham gia đi tham quan trải nghiệm. Ban tổ chức tính rằng, nếu trường thứ nhất có số học sinh tham gia tăng thêm $10\%$ và số học sinh trường thứ hai giảm đi $15\%$ thì số học sinh tham gia đi trải nghiệm không thay đổi. Tính số học sinh mỗi trường lúc ban đầu?

Ban tổ chức chuẩn bị $320$ chỗ ngồi cho học sinh khối 9 tham dự lễ kết nạp đoàn. Do số người đến dự vượt $100$ người so với số chỗ ngồi ban tổ chức chuẩn bị, nên ban tổ chức phải xếp mỗi dãy thêm $4$ ghế, và phải đặt thêm $1$ dãy ghế nữa mới đủ chỗ ngồi. Ban tổ chức lúc đầu xếp mấy dãy ghế và mỗi dãy bao nhiêu ghế?

Cho phương trình $x^2-(2m+1)x+m^2+m-2=0$. Chứng tỏ phương trình đã cho luôn có hai nghiệm phân biệt với mọi giá trị của $m$ và tìm $m$ để phương trình có hai nghiệm $x_1,\,x_2$ sao cho $A=x_1(x_2+5)$ đạt giá trị nhỏ nhất?

Bố bạn Minh thuê thợ đến sơn giả đá hai cây cột hình trụ kích thước như nhau với giá $360$ $000$ đồng/m². Biết rằng cột cao $3,6$ m và chu vi đáy cột bằng $1,5$ m. Bố bạn Minh phải trả bao nhiêu tiền công cho thợ sơn?

Cho tam giác $ABC$ có ba góc nhọn và $AB > AC$. Tam giác $ABC$ nội tiếp đường tròn $(O; R)$. Đường cao $AH$ của tam giác $ABC$ cắt đường tròn $(O; R)$ tại điểm thứ hai là $D$. Kẻ $DM$ vuông góc với $AB$ tại $M$.

a) Chứng minh tứ giác $BDHM$ nội tiếp đường tròn.

b) Chứng minh $DA$ là tia phân giác của $\widehat{MDC}$.

c) Gọi $N$ là hình chiếu vuông góc của $D$ lên đường thẳng $AC$, chứng minh ba điểm $M$, $H$, $N$ thẳng hàng.

Bác An có mảnh vườn hình vuông $ABCD$ có cạnh bằng $4$ m. Ở bốn góc vườn, bác An muốn trồng hoa vào các phần đất hình tam giác vuông bằng nhau (hình vẽ).

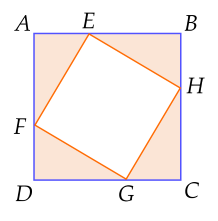
Tính khoảng cách từ góc vườn $A$ đến vị trí $E$ sao cho tứ giác $EFGH$ có chu vi nhỏ nhất.