Bài học cùng chủ đề
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Đề số 1 (phần tự luận 7 điểm) SVIP
Bài 1. (2 điểm) Thu gọn các biểu thức:
a) $\left(-12{{x}^{13}}{{y}^{15}}+6{{x}^{10}}{{y}^{14}} \right) \, : \, \left(-3{{x}^{10}}{{y}^{14}} \right);$
b) $\left(x-y \right)\left({{x}^{2}}-2x+y \right)-{{x}^{3}}+{{x}^{2}}y.$
Hướng dẫn giải:
a) $\left( -12{{x}^{13}}{{y}^{15}}+6{{x}^{10}}{{y}^{14}} \right) \, : \, \left( -3{{x}^{10}}{{y}^{14}} \right)$
$=\left( -12{{x}^{13}}{{y}^{15}} \right) \, : \, \left( -3{{x}^{10}}{{y}^{14}} \right)+\left( 6{{x}^{10}}{{y}^{14}} \right) \, : \, \left( -3{{x}^{10}}{{y}^{14}} \right)$
$=4{{x}^{3}}y-2.$
b) $\left( x-y \right)\left( {{x}^{2}}-2x+y \right)-{{x}^{3}}+{{x}^{2}}y$
$=x\left( {{x}^{2}}-2x+y \right)-y\left( {{x}^{2}}-2x+y \right)-{{x}^{3}}+{{x}^{2}}y$
$={{x}^{3}}-2{{x}^{2}}+xy-{{x}^{2}}y+2xy-{{y}^{2}}-{{x}^{3}}+{{x}^{2}}y$
$=-2{{x}^{2}}+3xy-{{y}^{2}}.$
Bài 2. (1 điểm) Phân tích đa thức thành nhân tử:
a) $xy+{{y}^{2}}-x-y;$
b) ${{\left({{x}^{2}}{{y}^{2}}-8 \right)}^{2}}-1;$
Hướng dẫn giải:
a) $xy+{{y}^{2}}-x-y$
$=\left( xy+{{y}^{2}} \right)-\left( x+y \right)$
$=y\left( x+y \right)-\left( x+y \right)$
$=\left( x+y \right)\left( y-1 \right).$
b) ${{\left( {{x}^{2}}{{y}^{2}}-8 \right)}^{2}}-1$
$=\left( {{x}^{2}}{{y}^{2}}-8-1 \right)\left( {{x}^{2}}{{y}^{2}}-8+1 \right)$
$=\left( {{x}^{2}}{{y}^{2}}-9 \right)\left( {{x}^{2}}{{y}^{2}}-7 \right)$
$=\left( xy-3 \right)\left( xy+3 \right)\left( {{x}^{2}}{{y}^{2}}-7 \right).$
$=\left( x-1 \right)\left( x+8 \right).$
Bài 3. (2 điểm) Một chiếc diều được mô tả như hình vẽ trên.

a) Tính số đo góc $D$ ở đuôi chiếc diều biết các góc ở đỉnh $\widehat{A}=\widehat{B}=\widehat{C}=102^\circ.$
b) Tính độ dài khung gỗ đường chéo $BD$ biết $OD=26,7$ cm (làm tròn kết quả đến hàng phần mười).
Hướng dẫn giải:
a) Số đo góc $D$ ở đuôi chiếc diều là: $\widehat{D}=360^\circ -\left( \widehat{A}+\widehat{B}+\widehat{C} \right)=360^\circ -\left( 102^\circ +102^\circ +102^\circ \right)=54^\circ .$
b) Xét $\Delta OAD$ vuông tại $O$, theo định lí Pythagore ta có:
$O{{A}^{2}}=A{{D}^{2}}-O{{D}^{2}}={{30}^{2}}-26,{{7}^{2}}=187,11$
Xét $\Delta OAB$ vuông tại $O,$ theo định lí Pythagore ta có:
$O{{B}^{2}}=A{{B}^{2}}-O{{A}^{2}}=17,{{5}^{2}}-187,11=119,14$
Do đó $OB=\sqrt{119,14}\approx 10,9$ (cm).
Suy ra $BD=OB+OD=10,9+26,7=37,6$ (cm).
Bài 4. (2 điểm) Một chiếc lều có dạng hình chóp tứ giác đều ở trại hè của học sinh có kích thước như hình trên.
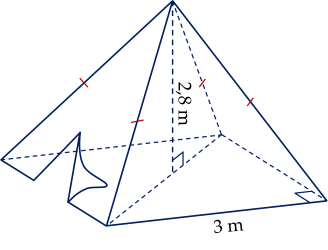
a) Tính thể tích không khí bên trong chiếc lều.
b) Tính số tiền mua vải phủ bốn phía và trải nền đất cho chiếc lều (coi các mép nối không đáng kể). Biết chiều cao của mặt bên xuất phát từ đỉnh của chiếc lều là $3,18$ m và giá vải là $15 \, 000$ đồng/m$^2$. Ngoài ra, nếu mua vải với hóa đơn trên $20$ m$^2$ thì được giảm giá $5\%$ trên tổng hóa đơn.
Hướng dẫn giải:
a) Diện tích đáy hình vuông của chiếc lều là:
$S_{\text{đáy}}={{3}^{2}}=9$ (m$^{2}$)
Thể tích không khí bên trong chiếc lều là:
$V=\dfrac{1}{3}S_{\text{đáy}}h=\dfrac{1}{3}. 9. 2,8=8,4$ (m$^3$).
b) Diện tích xung quanh của chiếc lều là:
${{S}_{xq}}=\dfrac{1}{2}.C.d=\dfrac{1}{2}.4.3.3,18=19,08$ (m$^2$)
Diện tích vải phủ bốn phía và trải nền đất cho chiếc lều là:
$S=9+19,08=28,08$ (m$^2$).
Do $28,08>20$ nên số tiền mua vải được giảm giá $5\%$ trên tổng hóa đơn.
Vậy số tiền mua vải là:
$28,08.15 \, 000.\left( 100\%-5\% \right)=400 \, 140$ (đồng).
