Bài học cùng chủ đề
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 0 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Đề kiểm tra giữa học kì I (đề số 3) SVIP
Yêu cầu đăng nhập!
Bạn chưa đăng nhập. Hãy đăng nhập để làm bài thi tại đây!
Mệnh đề phủ định của mệnh đề ''∃x∈R:5x−x2=0'' là
Cho hai tập hợp A và B. Hình nào sau đây minh họa A là tập con của B?
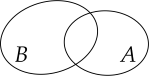
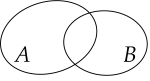
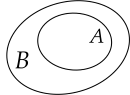
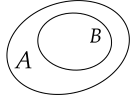
Cho hai tập hợp X={1;2;4;7;9} và Y={−1;0;7;10}. Tập hợp X∪Y có bao nhiêu phần tử?
Tập hợp P={x∈R−1<2x+1≤11} được viết lại dưới dạng đoạn, khoảng, nửa khoảng là
Đồ thị hàm số y=x2+2x−1 có tọa độ đỉnh là
Cho tam giác ABC có AB=5,BC=7,AC=8. Số đo của góc A là
Trong các cặp số sau, cặp số nào không là nghiệm của hệ bất phương trình {x+y−2≤02x−3y+2>0?
Mệnh đề phủ định của "5+4=10" là
Cho tập hợp A={x2+1x∈N,x≤5}. Tập hợp A viết bằng cách liệt kê phần tử là
Cho tập hợp A={1;2;3;4;5}. Số tập hợp X thỏa mãn A\X={1;3;5} và X\A={6;7} là
Cho tam giác ABC có b=7; c=5; cosA=53. Độ dài đường cao ha của tam giác ΔABC là
Cho tam giác ABC có bán kính đường tròn ngoại tiếp bằng 2. Nếu 2sinA+sinC=1 thì tổng AB+2BC bằng
Cho P⇔Q là mệnh đề đúng.
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) P⇒Q đúng. |
|
| b) Q⇒P sai. |
|
| c) P⇔Q sai. |
|
| d) P⇔Q sai. |
|
Cho các tập hợp CRA=[−3;8), CRB=(−5;2)∪(3;11).
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) A=(−∞;−3)∪[8;+∞). |
|
| b) B=(−∞;−5)∪(11;+∞). |
|
| c) A∩B=(−∞;−5)∪[8;+∞). |
|
| d) CR(A∩B)=(−5;11). |
|
Một xưởng sản xuất định lựa chọn hai loại máy chế biến loại I và loại II. Máy loại I mỗi ngày một máy chế biến được 300 kg sản phẩm, máy loại II mỗi ngày một máy chế biến được 450 kg sản phẩm. Biết rằng, để có lãi mỗi ngày xưởng phải sản xuất được nhiều hơn 50 tấn sản phẩm. Gọi x, y tương ứng là số lượng máy loại I và máy loại II xưởng chọn để sản xuất.
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) Khối lượng sản phẩm tạo ra trong một ngày từ số lượng máy trên là F(x;y)=30x+45y. |
|
| b) Để đảm bảo xưởng có lãi mỗi ngày, ta cần 6x+9y−1000>0. |
|
| c) Xưởng nên lựa chọn 50 máy chế biến loại I và 80 máy chế biến loại II để đảm bảo có lãi. |
|
| d) Nếu xưởng lựa chọn 70 máy chế biến loại I và 60 máy chế biến loại II sẽ không đảm bảo có lãi. |
|
Cho sinα=53 với 90∘<α<180∘.
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) cosα>0. |
|
| b) cos2α=2516. |
|
| c) cosα=54. |
|
| d) tanα=43. |
|
Trong đợt khảo sát nghề, giáo viên chủ nhiệm lớp 10D đưa ra ba nhóm ngành cho học sinh lựa chọn, đó là: Giáo dục, Y tế, Công nghệ thông tin. Học sinh có thể chọn từ một đến ba nhóm ngành nêu trên hoặc không chọn nhóm ngành nào trong ba nhóm ngành trên. Giáo viên chủ nhiệm thống kê theo từng nhóm ngành và được kết quả: có 6 học sinh chọn nhóm ngành Giáo dục, 9 học sinh chọn nhóm ngành Y tế, 10 học sinh chọn nhóm ngành Công nghệ thông tin, 22 học sinh không chọn nhóm ngành nào trong ba nhóm trên. Nếu thống kê số lượng học sinh chọn theo từng hai nhóm ngành được kết quả: có 3 học sinh chọn hai nhóm ngành Giáo dục và Y tế, 2 học sinh chọn hai nhóm ngành Y tế và Công nghệ thông tin, 3 học sinh chọn hai nhóm ngành Giáo dục và Công nghệ thông tin. Có bao nhiêu học sinh chọn cả ba nhóm ngành nêu trên biết lớp 10D có 40 học sinh?
Trả lời:
Để chuẩn bị cho đại hội chi đoàn 10A1, bạn Nga được phân công đi mua hoa để cắm vào 3 lọ, mỗi lọ cắm số hoa mỗi loại như nhau. Bạn Nga được lớp giao cho 200 nghìn đồng để mua nhưng đến quầy bán chỉ còn 2 loại hoa và đã mua đủ để cắm. Biết rằng một loại hoa có giá 15 nghìn đồng/bông và một loại có giá 20 nghìn/bông. Số tiền dư ra ít nhất có thể là bao nhiêu nghìn đồng?
Trả lời:
Cho bất phương trình x+3y−12≥0. Có bao nhiêu số nguyên m để cặp số (m2;m2+2m−2) không phải là nghiệm của bất phương trình đã cho.
Trả lời:
Một công ty TNHH trong một đợt quảng cáo và bán khuyến mãi hàng hóa cho sản phẩm mới của công ty cần thuê xe để chở trên 140 người và trên 9 tấn hàng. Nơi thuê chỉ có hai loại xe A và B. Trong đó xe loại A có 10 chiếc, xe loại B có 9 chiếc. Một chiếc xe loại A cho thuê với giá 4 triệu, loại B giá 3 triệu. Công ty có kế hoạch thuê x xe loại A và y xe loại B để chi phí vận chuyển là thấp nhất. Biết rằng xe A chỉ chở tối đa 20 người và 0,6 tấn hàng. Xe B chở tối đa 10 người và 1,5 tấn hàng. Tính x+y.
Trả lời:
Tìm giá trị nhỏ nhất của biết thức F=x−y với điều kiện ⎩⎨⎧0≤y≤4x≥0x−y−1≤0x+2y−10≤0.
Trả lời:
Hai chiếc tàu thủy P và Q cách nhau 100 m. Từ P và Q thẳng hàng với chân A của tháp hải đăng AB ở trên bờ biển người ra nhìn chiều cao AB của tháp dưới các góc BPA=15∘ và BQA=22∘. Tính chiều cao AB của tháp (Làm tròn kết quả đến chữ số thập phân thứ nhất của đơn vị mét)
Trả lời:

