Đề kiểm tra số 3 SVIP

Hướng dẫn giải:

1) a) Tổng số lượt sách trong tuần của thư viện đó: $15 + 35 + 30 + 20 = 100$ ( lượt)

b) Tần số tương đối số lượt mượn "sách tham khảo" là: $\dfrac{35}{100} = 35 \%$

2) Ta thấy các kết quả phép thử là đồng khả năng.

Các kết quả thuận lợi cho biến cố M là hình quạt ghi số 2, số 3, số 5, số 7

Xác suất của biến cố M là: $\dfrac{4}{8}=\dfrac{1}{2}$.

Hướng dẫn giải:

a) Thay $x=36$ ( thỏa mãn điều kiện) vào biểu thức $B$, ta được

$B=\dfrac{\sqrt{36}-3}{\sqrt{36}+1}=\dfrac{3}{7}$

b) Với $x \ge 0, \, x \ne 9$ ta có

$A=\dfrac{2\sqrt{x}}{\sqrt{x}+3}+\dfrac{\sqrt{x}+1}{\sqrt{x}-3}+\dfrac{3-11\sqrt{x}}{9-x}$

$=\dfrac{2\sqrt{x}\left( \sqrt{x}-3 \right)+\left( \sqrt{x}+1 \right)\left( \sqrt{x}+3 \right)+11\sqrt{x}-3}{\left( \sqrt{x}-3 \right)\left( \sqrt{x}+3 \right)} $

$=\dfrac{3x+9\sqrt{x}}{\left( \sqrt{x}-3 \right)\left( \sqrt{x}+3 \right)} $

$=\dfrac{3\sqrt{x}}{\sqrt{x}-3}$

c) Ta có $P=A. B=\dfrac{3\sqrt{x}}{\sqrt{x}-3}. \dfrac{\sqrt{x}-3}{\sqrt{x}+1}=\dfrac{3\sqrt{x}}{\sqrt{x}+1}$

Để $P=\dfrac{1}{2}$ thì $\dfrac{3\sqrt{x}}{\sqrt{x}+1}=\dfrac{1}{2} $

$6\sqrt{x}=\sqrt{x}+1 $

$5\sqrt{x}=1 $

$\sqrt{x}=\dfrac{1}{5}$

$x=\dfrac{1}{25}$ (thỏa mãn)

Vậy $x=\dfrac{1}{25}$ thì $P=\dfrac{1}{2}$.

Hướng dẫn giải:

Gọi vận tốc của xe máy là $x$ (km/h), ($x>0$)

Thời gian xe máy đi hết quãng đường $AB$ là: $\dfrac{180}{x}$ (h)

Vận tốc ô tô là: $x+5$ (km/h)

Thời gian ô tô đi hết quãng đường $AB$ là: $\dfrac{180}{x+5}$ (h)

Vì ô tô xuất phát sau xe máy $24$ phút $=\dfrac{2}{5}$ h nhưng vẫn đến $B$ cùng lúc nên ta có

$\dfrac{180}{x}-\dfrac{180}{x+5}=\dfrac{2}{5}$

Giải được $x=45$ (thỏa mãn), $x=-50$ (không thỏa mãn)

Vậy vận tốc xe máy là $45$ km/h.

Hướng dẫn giải:

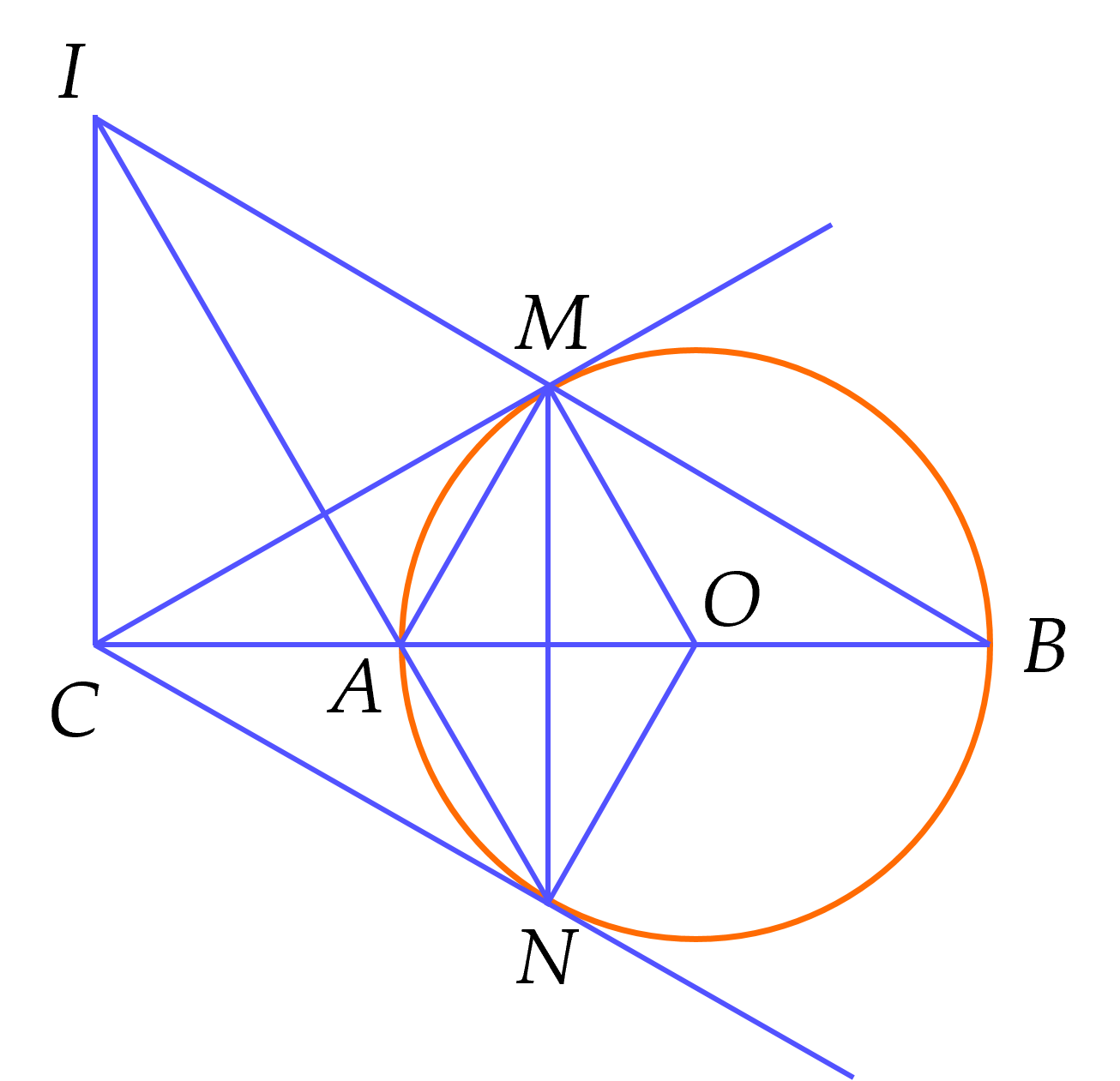
a) Xét $\Delta MAB$ có: $MO$ là trung tuyến và $MO=OB=OA=\dfrac{1}{2}AB$ nên $\Delta MAB$ vuông tại $M$.

Gọi $G$ là trung điểm của $IA$.

Chứng minh được $GI=GM=GA=GC$ nên bốn điểm $A, \, M, \, I, \, C$ cùng thuộc một đường tròn đường kính $IA$. '

b) Chứng minh được $\widehat{CIA}=\widehat{CBI}=\left( \widehat{CMA} \right)$

Xét $\Delta CIA$ và $\Delta CIB$ có:

$\widehat{ICA}$ chung;

$\widehat{CIA}=\widehat{CBI}$

Vậy $\Delta CIA \backsim \Delta CBI$ (g.g) 

Suy ra $CI^2=CA.CB$.

Hướng dẫn giải:

Phương trình $x^2-2mx+m^2-m-1=0$

Có $\Delta' = (-m)^2-1.(m^2-m-1)=m^2-m^2+m+1=m+1$

Phương trình có hai nghiệm $x_1$ và $x_2$ khi $\Delta' \ge 0$

$m+1 \ge 0$

$m \ge -1$

Áp dụng hệ thức Vietè ta có:

$x_1+x_2=2m$ và $x_1x_2=m^2-m-1$

Ta có: $x_1( x_1+2 )+x_2( x_2+2 )=10$

$x_{1}^{2}+2x_1+x_{2}^{2}+2x_2=10$

$x_{1}^{2}+x_{2}^{2}+2x_1+2x_2=10$

$( x_1+x_2 )^2-2x_1x_2+2( x_1+x_2 )=10$

$(2m)^2-2(m^2-m-1)+2.2m=10$

$4m^2-2m^2+2m+2+4m-10=0$

$2m^2+6m-8=0$

$m^2+3m-4=0$

Ta có: $a+b+c=1+3+(-4)=0$ nên phương trình có hai nghiệm: $m_1=1$ (thỏa mãn) và $m_2=-4$ (không thỏa mãn).

Vậy $m=1$ là giá trị cần tìm.

Hướng dẫn giải:

Ta gọi tên các đỉnh của hình chữ nhật như hình vẽ sau:

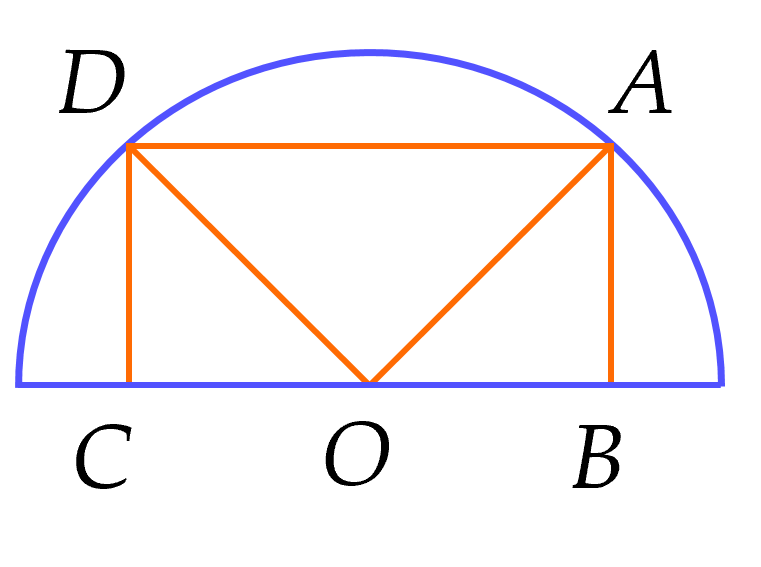
Đặt $AB=x$ (m) với $x>0.$

Do nửa đường tròn bán kính bằng $14$ m nên $OA=OD=14$ m.

Áp dụng định lí Pythagore trong tam giác vuông $OAB$ có:

$OA^2=BA^2+BO^2$

$14^2=x^2+BO^2$

$BO=\sqrt{196-x^2}$

Do đó $BC=2BO=2\sqrt{196-x^2}.$

Nên diện tích hình chữ nhật $ABCD$ là: $2x\sqrt{196-x^2}.$

Với hai số $a, \, b$ ta có: $(a-b)^2 \ge 0.$

Do đó $a^2+b^2 \ge 2ab.$

Áp dụng bất đẳng thức trên với hai số dương $x$ và $\sqrt{196-x^2}$ ta có:

$2x\sqrt{196-x^2} \le x^2+( \sqrt{196-x^2})^2=196$

Dấu bằng xảy ra khi $x=\sqrt{196-x^2}$ hay $x=7\sqrt{2}.$

Nên diện tích lớn nhất của khu vui chơi hình chữ nhật là $196$ m².