Đề thi giữa học kì I toán 10 Kết nối tri thức cấu trúc mới

Câu 1 (1đ):

Câu nào sau đây không phải là mệnh đề?

\pi

có phải là một số hữu tỉ không?

\sqrt{2}

là một số hữu tỉ.

2+2=5.

\dfrac{4}{2}=2.

Câu 2 (1đ):

Mệnh đề phủ định của "Bất phương trình $x-2<0$ vô nghiệm" là

"Bất phương trình

x-2\ge 0

có vô số nghiệm".

"Bất phương trình

x-2<0

có một nghiệm".

"Bất phương trình

x-2\ge 0

có nghiệm".

"Bất phương trình

x-2<0

có nghiệm".

Câu 3 (1đ):

Cho hai tập hợp $A$ và $B$ được minh họa bằng biểu đồ Ven như hình vẽ:

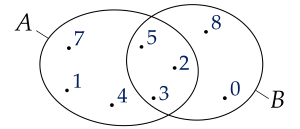
loading...

Khi đó tập hợp $C = A\cup B$ là

\left\{ 1;\,4;\,7 \right\}

.

\left\{ 0;\,1;\,2;\,3;\,4;\,5;\,7;\,8 \right\}

.

\left\{ 0;\,8 \right\}

.

\left\{ 2;\,3;\,5 \right\}

.

Câu 4 (1đ):

Cặp số nào sau đây là nghiệm của bất phương trình $2x-3y \le 6$ ?

(2 ; -3)

.

(4 ; -1)

.

(-2 ; -5)

.

(2 ; 1)

.

Câu 5 (1đ):

Hệ bất phương trình nào sau đây là hệ bất phương trình bậc nhất hai ẩn?

\left\{ \begin{aligned} & x+3y-6>0 \\ & 2|x|+y^2+4>0 \\ \end{aligned} \right.

.

\left\{ \begin{aligned} & x<0 \\ & y\ge 0 \\ \end{aligned} \right.

.

\left\{ \begin{aligned} & x+3y^3<0 \\ & x+y \le 1 \\ \end{aligned} \right.

.

\left\{ \begin{aligned} & x+2y-z>0 \\ & y<0 \\ \end{aligned} \right.

.

Câu 6 (1đ):

Giá trị $\cos 45^\circ + \sin 45^\circ$ bằng

\sqrt{3}

.

0

.

1

.

\sqrt{2}

.

Câu 7 (1đ):

Cho tam giác $ABC$ với $BC=a, \, AC=b, \, AB=c$ , bán kính đường tròn ngoại tiếp $R$ . Khẳng định nào sau đây đúng?

a=2R\cos A

.

a=R\sin A

.

a=2R\tan A

.

a=2R\sin A

.

Câu 8 (1đ):

Cho $\Delta ABC$ có $b=6, \, c=8, \, \widehat{A}=60^\circ$ . Độ dài cạnh $a$ là

2\sqrt{13}.

2\sqrt{37}.

\sqrt{20}.

3\sqrt{12}.

Câu 9 (1đ):

Cho các tập hợp $A=\Big\{ x \in \mathbb{N} \, \big| \, (4-x^2)(x^2-5x+4)=0 \Big\}$ ; $B=\Big\{x \in \mathbb{Z} \, \big| \, x$ là ước của $4\Big\}$ . Tập hợp $A \cap B$ là

\left\{ 2;\,4 \right\}

.

\left\{ -2;\,1;\,2;\,4 \right\}

.

\left\{ -4;\,-2;\,-1;\,1;\,2;\,4 \right\}

.

\left\{ 1;\,2;\,4 \right\}

.

Câu 10 (1đ):

Phần không tô màu trong hình vẽ dưới đây (không tính biên), biểu diễn tập nghiệm của hệ bất phương trình nào trong các hệ bất phương trình sau?

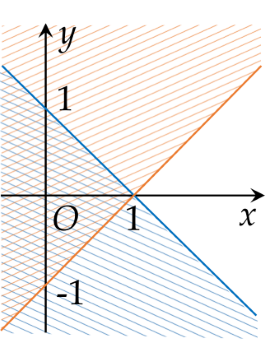
loading...

\left\{ \begin{aligned} & x-y<0 \\ & 2x-y>1 \\ \end{aligned} \right.

.

\left\{ \begin{aligned} & x-y>0 \\ & 2x-y>1 \\ \end{aligned} \right.

.

\left\{ \begin{aligned} & x-y<0 \\ & 2x-y<1 \\ \end{aligned} \right.

.

\left\{ \begin{aligned} & x-y>0 \\ & 2x-y<1 \\ \end{aligned} \right.

.

Câu 11 (1đ):

Cho $\sin x+\cos x=m$ . Giá trị của $M=\sin x.\cos x$ tính theo $m$ là

m^2-1

.

m^2+1

.

\dfrac{m^2+1}{2}

.

\dfrac{m^2-1}{2}

.

Câu 12 (1đ):

Cho biết $\sin \dfrac{\alpha }{3}=\dfrac{3}{5}.$ Giá trị của $P=3\sin^2 \dfrac{\alpha }{3}+5\cos^2 \dfrac{\alpha}{3}$ bằng

\dfrac{105}{25}.

\dfrac{107}{25}.

\dfrac{111}{25}.

\dfrac{109}{25}.

Câu 13 (1đ):

Cho ba tập hợp $C_{\mathbb{R}} M=\left(-\infty ;3 \right), \, C_{\mathbb{R}} N=\left(-\infty ;-3 \right)\cup \left(3;+\infty \right)$ và $C_{\mathbb{R}}P=\left(-2;3 \right]$ .

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) $N=\left( -3;3 \right)$ .
b) $P=\left(-\infty ;-2 \right] \cup \left(3;+\infty \right)$ .
c) $M \cap N= \varnothing$ .
d) $\left(M \cap N \right)\cup P=\left(-\infty ;-2 \right] \cup \left[ 3;+\infty \right)$ .

Câu 14 (1đ):

Một công ty viễn thông tính phí $1$ $000$ đồng mỗi phút gọi nội mạng và $2$ $000$ đồng mỗi phút gọi ngoại mạng. Gọi $x$ và $y$ lần lượt là số phút gọi nội mạng, ngoại mạng của Bình trong một tháng và Bình muốn số tiền phải trả cho tổng đài luôn thấp hơn $100$ nghìn đồng.

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Số tiền Bình phải trả cho cuộc gọi nội mạng mỗi tháng là $x$ (nghìn đồng), số tiền phải trả cho cuộc gọi ngoại mạng mỗi tháng là $2y$ (nghìn đồng) và $x \in \mathbb{N}, \, y\in \mathbb{N}$ .
b) $x+2y<100$ .
c) Nếu $50$ và $20$ lần lượt là số phút gọi nội mạng, ngoại mạng của Bình trong một tháng thì số tiền phải trả cho tổng đài thấp hơn $100$ nghìn đồng.
d) Nếu $50$ và $25$ lần lượt là số phút gọi nội mạng, ngoại mạng trong một tháng thì số tiền phải trả cho tổng đài vượt quá mục tiêu của Bình.

Câu 15 (1đ):

Cho hệ bất phương trình $\left\{ \begin{aligned}& 3x+2y\ge 9 \\& x-2y\le 3 \\ & x+y\le 6 \\ & x\quad \ge 1 \\ \end{aligned} \right.$ (I).

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Miền nghiệm của hệ bất phương trình (I) là một miền tam giác.
b) $(3;2)$ là một nghiệm của hệ bất phương trình (I).
c) $x=1; \, y=3$ là nghiệm của hệ bất phương trình (I) thỏa mãn $F=3x-y$ đạt giá trị lớn nhất.
d) $x=1; \, y=5$ là nghiệm của hệ bất phương trình (I) thỏa mãn $F=3x-y$ đạt giá trị nhỏ nhất.

Câu 16 (1đ):

Cho $\sin \alpha =\dfrac{1}{3}$ .

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) $\cos^2 \alpha =\dfrac{8}{9}$ .
b) $A=\sin^2 \alpha + 3\cos^2 \alpha =\dfrac{35}{9}$ .
c) $B=5\sin^2 \alpha - \cos^2 \alpha =-\dfrac{1}{3}$ .
d) $C=\sqrt{\sin^2 \alpha + 3\cos^2 \alpha}+\sqrt{\cos^2 \alpha - 7\sin^2 \alpha}=2$ .

Câu 17 (1đ):

Trong đợt khảo sát nghề, giáo viên chủ nhiệm lớp 10D đưa ra ba nhóm ngành cho học sinh lựa chọn, đó là: Giáo dục, Y tế, Công nghệ thông tin. Học sinh có thể chọn từ một đến ba nhóm ngành nêu trên hoặc không chọn nhóm ngành nào trong ba nhóm ngành trên. Giáo viên chủ nhiệm thống kê theo từng nhóm ngành và được kết quả: có $6$ học sinh chọn nhóm ngành Giáo dục, $9$ học sinh chọn nhóm ngành Y tế, $10$ học sinh chọn nhóm ngành Công nghệ thông tin, $22$ học sinh không chọn nhóm ngành nào trong ba nhóm trên. Nếu thống kê số lượng học sinh chọn theo từng hai nhóm ngành được kết quả: có $3$ học sinh chọn hai nhóm ngành Giáo dục và Y tế, $2$ học sinh chọn hai nhóm ngành Y tế và Công nghệ thông tin, $3$ học sinh chọn hai nhóm ngành Giáo dục và Công nghệ thông tin. Có bao nhiêu học sinh chọn cả ba nhóm ngành nêu trên biết lớp 10D có $40$ học sinh?

Trả lời:

Câu 18 (1đ):

Cho tam giác $ABC$ có $A(0;3); \, B(-1;2); \, C(2;1)$ . Có bao nhiêu giá trị nguyên của tham số $m$ để điểm $M\Big(m;\dfrac{2m-1}{2}\Big)$ nằm bên trong tam giác $ABC$ ?

Trả lời:

Câu 19 (1đ):

Một xưởng sản xuất hai loại sản phẩm là sản phẩm loại I và sản phẩm loại II:

▪️ Mỗi kg sản phẩm loại I cần $2$ kg nguyên liệu và $30$ giờ, thu lời (lãi) được $40$ nghìn đồng.

▪️ Mỗi kg sản phẩm loại II cần $4$ kg nguyên liệu và $15$ giờ, thu lời được $30$ nghìn đồng.

Xưởng có $200$ kg nguyên liệu và $1 \, 200$ giờ làm việc tối đa. Để có mức tiền lãi cao nhất, xưởng cần sản xuất $a$ sản phẩm loại I và $b$ sản phẩm loại II. Tính $a + b$ .

Trả lời:

Câu 20 (1đ):

Một tháp viễn thông cao $42$ m được dựng thẳng đứng trên một sườn dốc $34^\circ$ so với phương ngang. Từ đỉnh tháp người ta neo một sợi dây cáp xuống một điểm trên sườn dốc cách chân tháp $33$ m như hình vẽ.

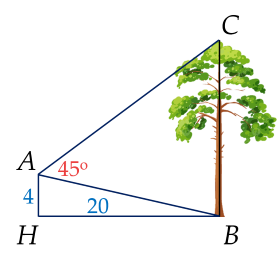
loading...

Tính chiều dài của sợi dây cáp đó. (Làm tròn kết quả đến hàng phần mười của đơn vị mét)

Trả lời:

Câu 21 (1đ):

Cho tam giác nhọn $ABC$ có $a=3, \, b=4$ và diện tích $S=3\sqrt{3}$ . Bán kính $R$ của đường tròn ngoại tiếp tam giác có dạng $R=\dfrac{\sqrt{m}}{n}$ , với $m, \, n\in \mathbb{N}, \, b\lt 5$ . Tính giá trị của biểu thức $T=m+n$ .

Trả lời:

Câu 22 (1đ):

Tìm giá trị nhỏ nhất của biểu thức $F(x;y)=x-y$ với điều kiện $\left\{ \begin{aligned}&x \ge 0 \\&y \ge 0 \\&x+y-3 \le 0 \\ \end{aligned} \right.$ .

Trả lời:

Bài học cùng chủ đề

Đề kiểm tra giữa học kì I (đề số 2) SVIP

Yêu cầu đăng nhập!

Bài học cùng chủ đề

Báo cáo học liệu

Mua học liệu

Mua học liệu:

Số dư ví của bạn: 0 coin - 0 Xu

Nếu mua học liệu này bạn sẽ bị trừ: 0 coin\Xu

Để nhận Coin\Xu, bạn có thể:

Chi tiết xem tại đây

Thông tin của bạn

Đề kiểm tra giữa học kì I (đề số 2) SVIP

Yêu cầu đăng nhập!

Truy vết IP log

Báo lỗi câu hỏi

Các khóa học có thể bạn quan tâm

Yêu cầu VIP