Bài học cùng chủ đề
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 0 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Đề kiểm tra giữa học kì II (đề số 1) SVIP
Yêu cầu đăng nhập!
Bạn chưa đăng nhập. Hãy đăng nhập để làm bài thi tại đây!
Kí hiệu K là một khoảng hoặc nửa khoảng hoặc một đoạn của R. Mệnh đề nào sau đây sai?
Hàm số nào dưới đây là một nguyên hàm của hàm số f(x)=x−1 trên (0;+∞)?
Họ nguyên hàm của hàm số f(x)=5x+41 là
Nếu 1∫2f(x)dx=6 và 1∫2g(x)dx=−2 thì 1∫2[f(x)−3g(x)]dx bằng
Gọi S là diện tích của hình phẳng giới hạn bởi các đường y=2x2+3x−5, y=0, x=−2, x=3. Khẳng định đúng là
Trong không gian Oxyz, vectơ n=(1;−1;−3) là một vectơ pháp tuyến của mặt phẳng nào sau đây?
Trong không gian với hệ tọa độ Oxyz, phương trình mặt phẳng qua A(−1;1;−2) và có vectơ pháp tuyến n=(1;−2;3) là
Tích phân 0∫ln2(ex+1)exdx bằng
Cho hàm số y=f(x). Biết f(0)=4 và f′(x)=2sin2x+3,∀x∈R, khi đó 0∫4πf(x)dx bằng
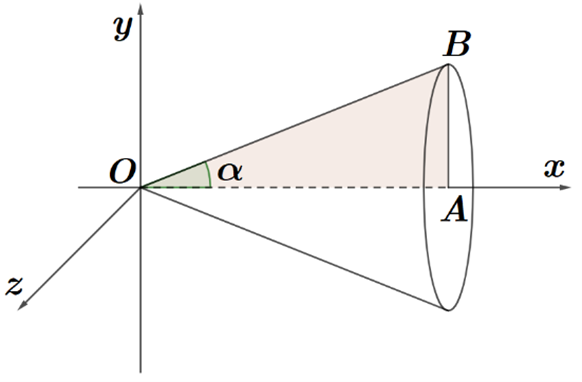
Cho tam giác vuông OAB có cạnh OA=a nằm trên trục Ox và AOB=3π. Khối tròn xoay sinh ra khi quay miền tam giác OAB quanh trục Ox có thể tích là
Trong không gian với hệ trục tọa độ Oxyz, cho A(1;2;3), B(3;4;4). Tất cả các giá trị của tham số m sao cho khoảng cách từ điểm A đến mặt phẳng (P):2x+y+mz−1=0 bằng độ dài đoạn thẳng AB là
Biết F(x) là một nguyên hàm của hàm số f(x)=x2. Biểu thức F′(25) bằng
Cho hàm số y=f(x)>0 liên tục trên R và f(1)=e3. Biết f′(x)=(2x−3).f(x),∀x∈R.
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) lnf(x)=x2−3x+C với C∈R. |
|
| b) f(x)=ex2−3x+5. |
|
| c) x=0 là một nghiệm của phương trình f(x)=e2x4−3x+4. |
|
| d) Phương trình f(x)=e2x4−3x+4 có bốn nghiệm phân biệt. |
|
Cho hàm số y=f(x) liên tục trên [-3;\,3] có đồ thị như hình vẽ, biết rằng f(x) tạo với trục hoành và hai đường thẳng x=−3, x=3 một hình phẳng (H) gồm hai phần có diện tích lần lượt là S1, S2. Xét tính đúng sai của 4 mệnh đề sau
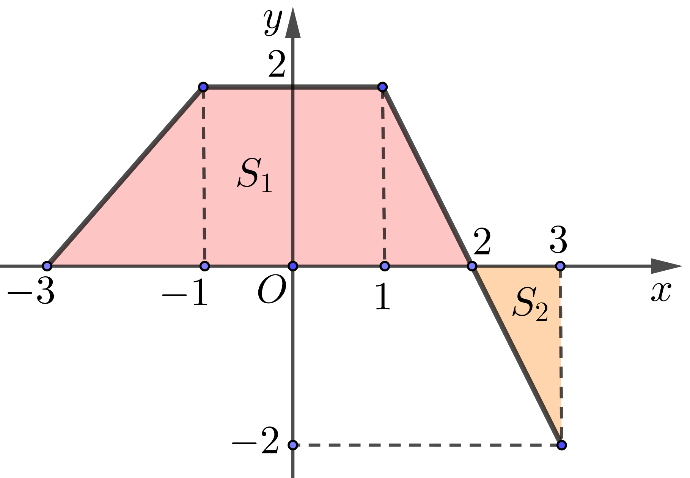
| a) S(H)=−3∫3f(x)dx. |
|
| b) S2=2∫3(−2x+4)dx=1. |
|
| c) S1=−3∫−1(x+3)dx+−1∫12dx+1∫2(−2x+4)dx. |
|
| d) S(H)=S1−2∫3(−2x+4)dx. |
|
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P):x+y+z+1=0 và hai điểm A(1;−1;2);B(2;1;1). Gọi (Q) là mặt phẳng chứa A,B và vuông góc với mặt phẳng (P).
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) Một vectơ pháp tuyến của mặt phẳng (Q) là (3;−2;−1). |
|
| b) Phương trình mặt phẳng (Q) là 3x−2y−z+3=0. |
|
| c) Điểm M(3;1;2) không thuộc mặt phẳng (Q). |
|
| d) Mặt phẳng (Q) song song với mặt phẳng (R):6x−4y−2z−6=0. |
|
Trong không gian Oxyz, cho hai mặt phẳng (P):x−3y+2z−1=0 và (Q):−2x+y+4z−3=0.
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) Mặt phẳng (P) song song mặt phẳng (Q). |
|
| b) Mặt phẳng (R) có phương trình 14x+8y+5z−2=0 cùng vuông góc với hai mặt phẳng (P) và (Q). |
|
| c) Mặt phẳng (α):2x−6y+4z−9=0 song song mặt phẳng (P):x−3y+2z−1=0 và cách mặt phẳng (P) một khoảng bằng 1. |
|
| d) Mặt phẳng (β) qua hai điểm A(1;0;1), B(2;−2;1) và vuông góc với mặt phẳng (Q) có một vectơ pháp tuyến là nβ=(8;4;3). |
|
Một viên đạn được bắn lên theo phương thẳng đứng với vận tốc ban đầu là 25 m/s, gia tốc trọng trường là 9,8 m/s2. Quãng đường viên đạn đi được từ lúc bắn cho đến khi chạm đất là bao nhiêu mét? (Làm tròn kết quả đến chữ số thập phân thứ nhất)
Trả lời:
Một chất điểm A xuất phát từ O, chuyển động thẳng với vận tốc biến thiên theo thời gian bởi quy luật v(t)=1801t2+1811t (m/s), trong đó t (giây) là khoảng thời gian tính từ lúc A bắt đầu chuyển động. Từ trạng thái nghỉ, một chất điểm B cũng xuất phát từ O, chuyển động thẳng cùng hướng với A nhưng chậm hơn 5 giây so với A và có gia tốc bằng a (m/s2) (a là hằng số). Sau khi B xuất phát được 10 giây thì đuổi kịp A. Vận tốc của B tại thời điểm đuổi kịp A bằng bao nhiêu?
Trả lời:
Trong lễ bàn giao công trình của lực lượng Cảnh Sát Biển Việt Nam, đơn vị thiết kế một cổng chào bằng phao chứa không khí ở bên trong, có hình dạng như một nửa cái Săm ô tô khi bơm căng. Cổng chào có chiều cao so với mặt sân là 8 m, phần chân của cổng chào tiếp xúc với mặt sân theo một đường tròn có đường kính là 2 m và bề rộng của cổng chào là 16 m. Bỏ qua độ dày của lớp vỏ cổng chào, mặt sân coi là bằng phẳng. Thể tích không khí chứa bên trong cổng chào bằng bao nhiêu? (làm tròn đến hàng phần mười).


Trả lời: m3.
Cho hình phẳng (H) được giới hạn bởi đường cong y=m2−x2 (m là tham số khác 0) và trục hoành. Khi (H) quay xung quanh trục hoành được khối tròn xoay có thể tích V. Có bao nhiêu giá trị nguyên của m để V<1000π?
Trả lời:
Trong không gian Oxyz, cho mặt phẳng (α):ax−y+2z+b=0 đi qua giao tuyến của hai mặt phẳng (P):x−y−z+1=0 và (Q):x+2y+z−1=0. Tính a+4b.
Trả lời:
Trong không gian Oxyz, cho mặt phẳng (α):2x+3y+z+1=0. Gọi (P) là mặt phẳng song song với (α), cắt các tia Ox,Oy,Oz lần lượt tại các điểm A, B, C sao cho thể tích khối tứ diện OABC bằng 6. Tính khoảng cách từ gốc tọa độ O đến mặt phẳng (P) (kết quả làm tròn đến hàng phần mười).
Trả lời:
