Đề ôn tập và kiểm tra giữa học kì I toán 11 cấu trúc mới mới nhất

Câu 1 (1đ):

Tập nghiệm của phương trình $\tan x=\sqrt{3}$ là

\Big\{ \dfrac{\pi }{6}+k\pi \, \Big| \,k\in \mathbb{Z} \Big\}

.

\Big\{ \dfrac{\pi }{3}+k\pi \, \Big| \, k\in \mathbb{Z} \Big\}

.

\Big\{ \dfrac{\pi }{3}+k2\pi \, \Big| \,k\in \mathbb{Z} \Big\}

.

\Big\{ \dfrac{\pi }{6}+k2\pi \, \Big| \,k\in \mathbb{Z} \Big\}

.

Câu 2 (1đ):

Cho dãy số $(u_n )$ với $u_n=\sin \dfrac{\pi }{n}$ . Khi đó, dãy số $(u_n)$

tăng.

bị chặn.

không bị chặn.

giảm.

Câu 3 (1đ):

Dãy số nào sau đây không phải cấp số cộng?

-8; \, -6; \, -4; \, -2;\, 0

.

\dfrac{1}{2}; \, \dfrac{3}{2}; \, \dfrac{5}{2}; \, \dfrac{7}{2}; \, \dfrac{9}{2}

.

1;\,1;\,1;\,1;\,1

.

3; \, 1; \, -1; \, -2; \, -4

.

Câu 4 (1đ):

Câu 5 (1đ):

Câu 6 (1đ):

Hàm số nào dưới đây là hàm số lẻ?

y=\tan x

.

y=\cos x

.

y={{\sin }^{2}}x

.

y={{\cot }^{2}}x

.

Câu 7 (1đ):

Trên khoảng $\left(-6\pi ;-5\pi \right)$ , hàm số nào sau đây luôn nhận giá trị dương?

y=\tan x

y=\cos x

.

y=\cot x

.

y=\sin x

.

Câu 8 (1đ):

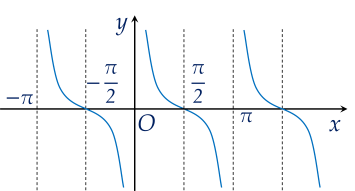
Họ nghiệm của phương trình $\sin x=\sin \dfrac{\pi }{5}$ là

\left[ \begin{aligned} & x=\dfrac{\pi }{5}+k2\pi \\ & x=\dfrac{4\pi }{5}+l2\pi \\ \end{aligned} \right.,\,k, \, l\in \mathbb{Z}

.

\left[ \begin{aligned} & x=\dfrac{\pi }{5}+k\pi \\ & x=-\dfrac{\pi }{5}+l\pi \\ \end{aligned} \right.,\,k, \, l\in \mathbb{Z}

.

\left[ \begin{aligned} & x=\dfrac{\pi }{5}+k2\pi \\ & x=-\dfrac{\pi }{5}+l2\pi \\ \end{aligned} \right.,\,k, \, l\in \mathbb{Z}

.

\left[ \begin{aligned} & x=\dfrac{\pi }{5}+k\pi \\ & x=\dfrac{4\pi }{5}+l\pi \\ \end{aligned} \right.,\,k, \, l \in \mathbb{Z}

.

Câu 9 (1đ):

Cho mẫu số liệu ghép nhóm về chiều cao của $20$ học sinh lớp lá như sau:

Chiều cao (cm)	$\left[ 70;79 \right)$	$\left[ 79;88 \right)$	$\left[ 88;97 \right)$	$\left[ 97;106 \right)$	$\left[ 106;115 \right)$
Số học sinh	$1$	$2$	$4$	$10$	$3$

Trung vị của mẫu số liệu ghép nhóm này là

M_e=\dfrac{1 \, 123}{10}

.

M_e=\dfrac{997}{10}

.

M_e=\dfrac{907}{10}

.

M_e=\dfrac{1 \, 087}{10}

.

Câu 10 (1đ):

Phương trình $\sqrt{3}\sin \left(2x+\dfrac{\pi }{6} \right)-\cos \left(2x+\dfrac{\pi }{6} \right)=1$ tương đương với phương trình nào sau đây?

\sin 2x=-\dfrac{1}{2}

.

\sin 2x=\dfrac{1}{2}

.

\sin \left(2x+\dfrac{\pi }{6} \right)=1

.

\sin \left(2x+\dfrac{\pi }{3} \right)=\dfrac{1}{2}

.

Câu 11 (1đ):

Tổng $n$ số hạng đầu tiên của một cấp số cộng cho bởi $S_{n} = 3n^{2} - n$ . Công sai của cấp số cộng đó là

d = 6

.

d = 7

.

d = 5

.

d = 4

.

Câu 12 (1đ):

Cho một cấp số nhân có các số hạng đều không âm thỏa mãn $u_2=12$ và $u_4=192$ . Tổng của $9$ số hạng đầu tiên của cấp số nhân đó là

1-4^9

.

-4(1-4^9)

.

4^9-1

.

4(1-4^9)

.

Câu 13 (1đ):

Cho mẫu số liệu điểm môn Toán của một nhóm học sinh như sau:

Điểm	$\left[ 6 ; 7 \right)$	$\left[ 7 ; 8 \right)$	$\left[ 8 ; 9 \right)$	$\left[ 9 ; 10 \right]$
Số học sinh	$8$	$7$	$10$	$5$

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Mẫu số liệu đã cho là mẫu số liệu ghép nhóm.
b) Cỡ mẫu của mẫu số liệu là $30$ .
c) Điểm trung bình của các học sinh là $7,9$ .
d) Mốt của mẫu số liệu là $10$ .

Câu 14 (1đ):

Cho hai đồ thị hàm số $y=\sin \Big(x+\dfrac{\pi }{4}\Big)$ và $y=\sin x$ .

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Phương trình hoành độ giao điểm của hai đồ thị hàm số: $\sin \Big(x+\dfrac{\pi }{4}\Big)=\sin x$ .
b) Hoành độ giao điểm của hai đồ thị là $x=\dfrac{3\pi }{8}+k\pi, \,(\, k\in \mathbb{Z})$ .
c) Khi $x \in \,[0;2\pi ]$ thì hai đồ thị hàm số cắt nhau tại ba điểm.
d) Khi $x\in \,[0;2\pi ]$ thì toạ độ giao điểm của hai đồ thị hàm số là: $\Big(\dfrac{5\pi }{8};\sin \dfrac{5\pi }{8} \Big)$ ; $\Big(\dfrac{7\pi }{8};\sin \dfrac{7\pi }{8} \Big)$ .

Câu 15 (1đ):

Giá của một chiếc xe ô tô lúc mới mua là $680$ triệu đồng. Cứ sau mỗi năm sử dụng, giá của chiếc xe ô tô giảm $50$ triệu đồng. Gọi $u_n$ là giá của chiếc ô tô trong năm thứ $n$ sử dụng.

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) $u_2=630$ .
b) Dãy số $(u_n)$ là cấp số cộng với công sai $d=50$ .
c) Giá của chiếc ô tô sau $3$ năm sử dụng lớn hơn $500$ triệu đồng.
d) Sau ít nhất $8$ năm sử dụng thì giá của chiếc ô tô nhỏ hơn một nửa giá trị ban đầu của nó.

Câu 16 (1đ):

Vào năm con gái được $4$ tuổi, một người cha chuẩn bị gửi tiết kiệm đầu mỗi năm một số tiền $x$ , $\left(x\in \mathbb{N} \right)$ để đến năm con gái $18$ tuổi sẽ có được $200$ triệu cho con gái đi học đại học. Hiện tại lãi suất tiền gửi hàng năm là $4,8\%$ /năm. Giả sử lãi suất này được giữ ổn định.

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Tổng số tiền thu về sau $14$ năm là một cấp số nhân có $q=(1+4,8\%)$ .
b) Số tiền tiết kiệm được sau năm thứ nhất là $x + x.(1+4,8\%)$ .
c) $x=9$ .
d) Đến năm con gái được $10$ tuổi, người cha dự định khi con gái được $18$ tuổi sẽ mua thêm cho con gái một chiếc xe máy trị giá $50$ triệu đồng. Do đó, kể từ thời điểm đầu năm con gái được $10$ tuổi người này cần gửi tiết kiệm $y$ triệu đồng đến khi con gái $18$ tuổi, $\left(y\in \mathbb{N} \right)$ . Giá trị nhỏ nhất của $y=15$ .

Câu 17 (1đ):

Trong môn cầu lông, khi phát cầu, người chơi cần đánh cầu qua khỏi lưới sang phía sân đối phương và không được để cho cầu rơi ngoài biên. Trong mặt phẳng toạ độ $Oxy$ , chọn điểm có tọa độ $\left(O;y_0\right)$ là điểm xuất phát thì phương trình quỹ đạo của cầu lông khi rời khỏi mặt vợt là: $y=\dfrac{-g.x^2}{2.v_{0}^{2}.\cos^{2}\alpha}+\tan (\alpha).x+y_0$ ; trong đó: $g$ là gia tốc trọng trường (thường được chọn là $9,8$ m/s $^{2}$ ; $\alpha$ là góc phát cầu (so với phương ngang của mặt đất); ${{v}_{0}}$ là vận tốc ban đầu của cầu; ${{y}_{0}}$ là khoảng cách từ vị trí phát cầu đến mặt đất. Quỹ đạo chuyển động của quả cầu lông là một parabol như hình vẽ.

loading...

Một người chơi cầu lông đang đứng khoảng cách từ vị trí người này đến vị trí cầu rơi chạm đất (tầm bay xa) là $6,68$ m. Người chơi đó đã phát cầu với góc tối đa khoảng bao nhiêu độ so với mặt đất? (biết cầu rời mặt vợt ở độ cao $0,7$ m so với mặt đất và vận tốc xuất phát của cầu là $8$ m/s, bỏ qua sức cản của gió và xem quỹ đạo của cầu luôn nằm trong mặt phẳng thẳng đứng, làm tròn kết quả tới hàng đơn vị).

Trả lời:

Câu 18 (1đ):

Gọi $n$ là số nghiệm của phương trình $\sin \left(2x+{{30}^\circ} \right)=\dfrac{\sqrt{3}}{2}$ trên khoảng $\left(-{{180}^\circ};{{180}^\circ} \right)$ . Tìm $n$ .

Trả lời:

Câu 19 (1đ):

Một chiếc đu quay có bán kính $75$ m, tâm của vòng quay ở độ cao $90$ m, thời gian thực hiện mỗi vòng quay của đu quay là $30$ phút.

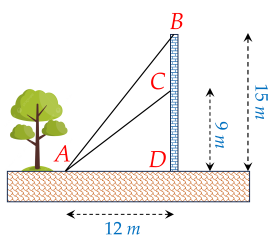
loading...

Nếu một người vào cabin tại vị trí thấp nhất của vòng quay, thì sau $20$ phút quay, người đó ở độ cao bao nhiêu mét? (làm tròn kết quả tới hàng phần mười)

Trả lời:

Câu 20 (1đ):

Cho dãy số $(u_n )$ xác định bởi $\left\{ \begin{aligned} & u_1=1 \\ & u_{n+1}=u_n-2(n+1 ) \\ \end{aligned} \right.\,$ với $n\ge 1$ . Tính giá trị biểu thức $S=\dfrac{3}{3-u_1}+\dfrac{3}{3-u_2}+\dfrac{3}{3-u_3}+\,...\,+\dfrac{3}{3-u_{20}}$ (làm tròn kết quả đến chữ số thập phân thứ hai)

Trả lời:

Câu 21 (1đ):

Ông Sơn trồng cây trên một mảnh đất hình tam giác theo quy luật: ở hàng thứ nhất có $1$ cây, hàng thứ hai có $2$ cây, hàng thứ ba có $3$ cây…, ở hàng thứ $n$ có $n$ cây. Biết rằng ông đã trồng hết $11 \, 325$ cây. Số hàng cây được trồng theo cách trên là bao nhiêu?

Trả lời:

Câu 22 (1đ):

Trong thời gian liên tục $25$ năm, một người lao động luôn gửi đúng $4 \, 000 \, 000$ đồng vào một ngày cố định của tháng ở ngân hàng $M$ với lãi suất không thay đổi trong suốt thời gian gửi tiền là $0,6\%$ tháng. Gọi $A$ đồng là số tiền người đó có được sau $25$ năm. Tính $A$ , đơn vị triệu đồng, làm tròn tới hàng đơn vị.

Trả lời:

Bài học cùng chủ đề

Đề kiểm tra giữa học kì I (đề số 1) SVIP

Yêu cầu đăng nhập!

Bài học cùng chủ đề

Báo cáo học liệu

Mua học liệu

Mua học liệu:

Số dư ví của bạn: 0 coin - 0 Xu

Nếu mua học liệu này bạn sẽ bị trừ: 0 coin\Xu

Để nhận Coin\Xu, bạn có thể:

Chi tiết xem tại đây

Thông tin của bạn

Đề kiểm tra giữa học kì I (đề số 1) SVIP

Yêu cầu đăng nhập!

Truy vết IP log

Báo lỗi câu hỏi

Các khóa học có thể bạn quan tâm

Yêu cầu VIP