Đề kiểm tra học kì I (đề số 2)

Câu 1 (1đ):

Nghiệm của phương trình $2\cos \left(x-15^\circ \right)-1=0$ là

\left[ \begin{aligned} & x=60^\circ +k360^\circ \\ & x=-60^\circ +k360^\circ \\ \end{aligned} \right.

,

k\in \mathbb{Z}

.

\left[ \begin{aligned} & x=75^\circ +k360^\circ \\ & x=-45^\circ +k360^\circ \\ \end{aligned} \right.

,

k\in \mathbb{Z}

.

\left[ \begin{aligned}& x=75^\circ +k360^\circ \\& x=135^\circ +k360^\circ \\ \end{aligned} \right.

,

k\in \mathbb{Z}

.

\left[ \begin{aligned} & x=45^\circ +k360^\circ \\ & x=-45^\circ +k360^\circ \\ \end{aligned} \right.

,

k\in \mathbb{Z}

.

Câu 2 (1đ):

Cho cấp số cộng $(u_n)$ có $u_1=-3$ và công sai $d=3$ . Số hạng $u_{10}$ là

u_{10}=-24

.

u_{10}=24

.

u_{10}=27

.

u_{10}=-{{3.3}^{9}}

.

Câu 3 (1đ):

Gọi $i$ là nhóm có tần số lớn nhất. Gọi $u,\ g,\ {{n}_{i}}$ lần lượt là đầu mút trái, độ dài và tần số của nhóm $i$ ; $\ {{n}_{i-1}},\ \ {{n}_{i+1}}$ lần lượt là tần số của nhóm $i-1,\$ nhóm $i+1$ . Gọi $M_0$ là Mốt của mẫu số liệu ghép nhóm, mệnh đề nào sau đây đúng?

M_0=u+\left(\dfrac{{{n}_{i}}-{{n}_{i-1}}}{2{{n}_{i}}-{{n}_{i-1}}-{{n}_{i+1}}} \right).g

.

M_0=u+\left(\dfrac{{{n}_{i}}.{{n}_{i-1}}}{2{{n}_{i}}-{{n}_{i+1}}-{{n}_{i-1}}} \right).g

.

M_0=u.\left(\dfrac{{{n}_{i}}-{{n}_{i-1}}}{2{{n}_{i}}-{{n}_{i-1}}-{{n}_{i+1}}} \right)-g

.

M_0=u+\left(\dfrac{{{n}_{i+1}}-{{n}_{i-1}}}{2{{n}_{i}}-{{n}_{i-1}}-{{n}_{i+1}}} \right).g

.

Câu 4 (1đ):

Cho hình chóp $S.ABCD$ có $AD$ không song song với $BC.$ Gọi $M, \, N,$ $P, \, Q, \, R,\, T$ lần lượt là trung điểm $AC, \, BD, \, BC, \, CD, \, SA, \, SD.$

Cặp đường thẳng nào sau đây song song với nhau?

PQ

và

RT.

MP

và

RT.

MN

và

RT.

MQ

và

RT.

Câu 5 (1đ):

Trong các mệnh đề sau, mệnh đề nào sai?

Một đường thẳng có thể trùng với hình chiếu của nó.

Hình chiếu song song của hai đường thẳng chéo nhau có thể song song với nhau.

Hình chiếu song song của hai đường thẳng chéo nhau có thể trùng nhau.

Một tam giác bất kì đều có thể xem là hình biểu diễn của một tam giác cân.

Câu 6 (1đ):

Hai đường thẳng $a$ và $b$ nằm trong $(\alpha)$ . Hai đường thẳng $a'$ và $b'$ nằm trong mặt phẳng $(\beta)$ . Mệnh đề nào sau đây đúng?

A

Nếu

a

//

a'

và

b

//

b'

thì

(\alpha)

//

(\beta)

.

B

Nếu

a

cắt

b

,

a'

cắt

b'

và

a

//

a'

và

b

//

b'

thì

(\alpha)

//

(\beta)

.

C

Nếu

(\alpha)

//

(\beta)

thì

a

//

a'

và

b

//

b'

.

D

Nếu

a

//

b

và

a'

//

b'

thì

(\alpha)

//

(\beta)

.

Câu 7 (1đ):

Giá trị của $\lim 5^n$ là

-\infty

.

+\infty

.

2

.

-2

.

Câu 8 (1đ):

Cho cấp số nhân có số hạng thứ hai là $u_2=4$ , công bội $q=\dfrac12$ . Giá trị của $u_{20}$ bằng

\Big(\dfrac{1}{2} \Big)^{17}

.

\Big(\dfrac{1}{2} \Big)^{19}

.

\Big(\dfrac{1}{2} \Big)^{16}

.

\Big(\dfrac{1}{2} \Big)^{20}

.

Câu 9 (1đ):

$L=\underset{x \to 1}{\mathop{\lim}}\dfrac{x^2+3x-4}{x-1}$ bằng

-5

.

0

.

-3

.

5

.

Câu 10 (1đ):

Cho hàm số $y = f(x)=\left\{ \begin{aligned} & x^2+x\,\, khi\,\,x\ge 1 \\ & 3x+1\,\,khi\,\,x\lt 1 \\ \end{aligned} \right.$ . Giá trị $\underset{x \to 1^+}{\mathop{\lim}}f(x)$ bằng

4

.

2

.

1

.

3

.

Câu 11 (1đ):

$\underset{x \to +\infty }{\mathop{\lim}}(\sqrt{x+1}-\sqrt{x-3})$ bằng

2

.

-\infty

.

+\infty

.

0

.

Câu 12 (1đ):

Hàm số $y = f(x)=\left\{ \begin{aligned} & \dfrac{x^2-4}{x-2} \, \, khi \, \ ,x\ne 2 \\ &5 \, \, khi \, \, x=2 \\ \end{aligned} \right.$ gián đoạn tại điểm nào trong các điểm sau?

x=0

.

x=1

.

x=-2

.

x=2

.

Câu 13 (1đ):

Cho dãy số $(u_n)$ biết $u_n=\dfrac{2n+1}{n+2}, \, n \in \mathbb{N}^*$ .

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Hai số hạng đầu của dãy là $u_1=1$ và $u_2=\dfrac{5}{3}$ .
b) Dãy số $(u_n)$ là một dãy số tăng.
c) Dãy số $(u_n)$ bị chặn trên bởi $\dfrac{33}{17}$ .
d) Dãy số $(u_n)$ có duy nhất một số hạng nguyên.

Câu 14 (1đ):

Điểm kiểm tra giữa học kì I của lớp 11A1 được thống kê như bảng dưới:

Khoảng điểm	Số học sinh
$\big[5 \, ; \, 6\big)$	$3$
$\big[6 \, ; \, 7\big)$	$5$
$\big[7 \, ; \, 8\big)$	$10$
$\big[8 \, ; \, 9\big)$	$6$
$\big[9 \, ; \, 10\big)$	$2$

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Cỡ mẫu của số liệu là $n=25$ .
b) Nhóm chứa mốt của số liệu là $\big[ 7;8 \big)$ .
c) Số học sinh đạt điểm khá (từ $8$ điểm trở lên) là $18$ .
d) Tứ phân vị thứ nhất của mẫu số liệu trên là: $Q_1=6,7$ .

Câu 15 (1đ):

Cho hình chóp $S.ABCD$ có đáy là hình bình hành. Gọi $O$ là giao điểm của $AC$ và $BD$ ; $M$ , $N$ lần lượt là trung điểm của $SB$ , $SD$ ; $P$ thuộc đọan $SC$ và không là trung điểm của $SC$ .

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Giao tuyến của hai mặt phẳng $(SAC)$ và $(SBD)$ là $SO$ .
b) Giao điểm $E$ của đường thẳng $SO$ và mặt phẳng $(MNP)$ là giao điểm của $MN$ và $SO$ .
c) Giao điểm $Q$ đường thẳng $SA$ và mặt phẳng $(MNP)$ là giao điểm của $PE$ và $SO$ .
d) Gọi $I$ , $J$ , $K$ lần lượt là giao điểm của $QM$ và $AB$ , $QP$ và $AC$ , $QN$ và $AD$ . Khi đó, $I$ , $J$ , $K$ thẳng hàng.

Câu 16 (1đ):

Trong hồ có chứa $6 \, 000$ lít nước ngọt (có nồng độ muối xem như bằng $0$ ). Người ta bơm nước biển có nồng độ muối là $30$ gam/lít vào hồ với tốc độ $15$ lít/phút. Biết rằng, nồng độ muối trong dung dịch được tính bằng công thức $C=\dfrac{m}{V}$ .

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Sau thời gian $t$ (phút), lượng nước được bơm vào hồ là $V(t)=15t$ (lít).
b) Khối lượng muối được bơm vào hồ sau thời gian $t$ (phút) là $m=450t$ (g).
c) Nồng độ muối trong hồ sau thời gian $t$ phút là $C(t)=\dfrac{15t}{6 \, 000+450t}$ .
d) Khi thời gian $t$ phút càng lớn, nồng độ muối trong hồ sẽ càng cao nhưng không vượt quá $C(t)=15$ (g/lít).

Câu 17 (1đ):

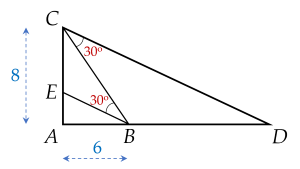
loading...

Từ một vị trí $A$ , người ta buộc hai sợi cáp $AB$ và $AC$ đến một cái trụ cao $15$ m, được dựng vuông góc với mặt đất, chân trụ ở vị trí $D$ . Biết $CD=9$ m và $AD=12$ m. Tìm góc nhọn $\alpha =\widehat{BAC}$ tạo bởi hai sợi dây cáp đó, đồng thời tính gần đúng $\alpha$ (làm tròn đến hàng phần mười, đơn vị độ).

Trả lời:

Câu 18 (1đ):

Nguời ta thiết kế một cái tháp gồm $10$ tầng theo cách: Diện tích bề mặt trên của mỗi tầng bằng nửa diện tích bề mặt trên của tầng ngay bên dưới và diện tích bề mặt của tầng $1$ bằng nửa diện tích bề mặt đế tháp. Biết diện tích bề mặt đế tháp là $12 \, 288$ m $^2$ , tính diện tích bề mặt trên cùng của tháp (đơn vị mét vuông).

Trả lời:

Câu 19 (1đ):

Khảo sát số lần sử dụng Facebook của một người thực hiện mỗi ngày trong $30$ ngày được lựa chọn ngẫu nhiên được thống kê trong bảng sau:

Số lần sử dụng facebook	Số ngày
$\big[3 \, ; \, 5\big]$	$2$
$\big[6 \, ; \, 8\big]$	$5$
$\big[9 \, ; \, 11\big]$	$11$
$\big[12 \, ; \, 14\big]$	$8$
$\big[15 \, ; \, 17\big]$	$4$

Tìm mốt của mẫu số liệu ghép nhóm trên?

Trả lời:

Câu 20 (1đ):

Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình bình hành tâm $O$ . Gọi $M$ , $N$ lần lượt là trung điểm của các cạnh $CD$ và $SD$ . Biết rằng mặt phẳng $(BMN)$ cắt đường thẳng $SA$ tại $P$ . Tỉ số $\dfrac{SP}{SA}$ bằng bao nhiêu? (Làm tròn kết quả đến hàng trăm)

Trả lời:

Câu 21 (1đ):

Phương trình $-\sin^3 x+3\sin x+1=0$ có tất cả bao nhiêu nghiệm thuộc khoảng $(-\pi ;2\pi)$ ?

Trả lời:

Câu 22 (1đ):

Nhiệt độ sấy mít dẻo bằng máy sấy nhiệt được điều khiển tăng từ $30^\circ$ C mỗi phút tăng $3^\circ$ C trong $12$ phút, sau đó giảm mỗi phút $1^\circ$ C trong $6$ phút. Hàm số biểu thị nhiệt độ (tính theo $^\circ$ C) trong máy sấy nhiệt theo thời gian $t$ (tính theo phút) có dạng: $T(t)=\left\{ \begin{aligned} & 30+3t \,\,khi\,\, 0 \le t \le 12 \\ & m-t \,\,khi\,\, 12\lt t \le 18 \\ \end{aligned} \right.$ ( $m$ là hằng số). Biết rằng, $y = T(t)$ là hàm số liên tục trên tập xác định. Tìm $m$ .

Trả lời:

Bài học cùng chủ đề

Đề kiểm tra học kì I (đề số 2) SVIP

Yêu cầu đăng nhập!

Bài học cùng chủ đề

Báo cáo học liệu

Mua học liệu

Mua học liệu:

Số dư ví của bạn: 0 coin - 0 Xu

Nếu mua học liệu này bạn sẽ bị trừ: 0 coin\Xu

Để nhận Coin\Xu, bạn có thể:

Chi tiết xem tại đây

Thông tin của bạn

Đề kiểm tra học kì I (đề số 2) SVIP

Yêu cầu đăng nhập!

Truy vết IP log

Báo lỗi câu hỏi

Các khóa học có thể bạn quan tâm

Yêu cầu VIP