Đề kiểm tra học kì I (đề số 2)

Câu 1 (1đ):

Một sinh viên đo độ dài của một số lá dương xỉ trưởng thành, kết quả như sau:

Lớp độ dài (cm)	Tần số
$\big[10 \, ; \, 20\big)$	$8$
$\big[20 \, ; \, 30\big)$	$6$
$\big[30 \, ; \, 40\big)$	$24$
$\big[40 \, ; \, 50\big)$	$10$

Khoảng biến thiên của mẫu số liệu ghép nhóm trên là

35

.

45

.

40

.

30

.

Câu 2 (1đ):

Trong không gian $Oxyz$ , cho ba vectơ $\overrightarrow{a}=(1 ;-1 ; 2), \overrightarrow{b}=(3 ; 0 ;-1)$ và $\overrightarrow{c}=(-2 ; 5 ; 1)$ . Vectơ $\overrightarrow{d}=\overrightarrow{a}+\overrightarrow{b}-\overrightarrow{c}$ có tọa độ là

(6 ;-6 ; 0)

.

(6 ; 0 ;-6)

.

(0 ; 6 ;-6)

.

(-6 ; 6 ; 0)

.

Câu 3 (1đ):

Trong không gian $O x y z$ , cho vectơ $\overrightarrow{a}=2 \overrightarrow{i}+\overrightarrow{j}-2 \overrightarrow{k}$ . Độ dài của vectơ $\overrightarrow{a}$ bằng

4 .

1 .

5 .

3.

Câu 4 (1đ):

Trong không gian với hệ tọa độ $Oxyz$ , cho $\overrightarrow{OM}=(1;5;2)$ , $\overrightarrow{ON}=(3;7;-4)$ , $K(-1;3;1)$ . Gọi $P$ là điểm đối xứng với $M$ qua $N$ . Tọa độ vectơ $\overrightarrow{KP}$ là

\overrightarrow{KP}=(8;6;-11)

.

\overrightarrow{KP}=(6;6;-11)

.

\overrightarrow{KP}=(3;3;-2)

.

\overrightarrow{KP}=(6;6;-4)

.

Câu 5 (1đ):

Cho hàm số $y=-\dfrac{2x^3}{3}+x^2+4x-2$ , gọi đồ thị của hàm số là $(C)$ . Đường thẳng nào sau đây tiếp xúc với đồ thị hàm số $(C)$ ?

y=-\dfrac{3}{4}x-\dfrac{5}{2}

.

y=-\dfrac{3}{4}x-\dfrac{1}{2}

.

y=-\dfrac{3}{4}x+\dfrac{1}{2}

.

y=-\dfrac{3}{4}x-\dfrac{7}{2}

.

Câu 6 (1đ):

Cho hàm số $y=f(x)$ có đồ thị trên đoạn $[-1;1]$ là đường cong như hình vẽ.

Cho hàm số $y=f(x)$ có đồ thị trên đoạn $[-1;1]$

Gọi $M, \, m$ lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của $f(x)$ trên đoạn $[-1;1]$ . Khi đó biểu thức $M-m$ bằng

2

.

4

.

3

.

0

.

Câu 7 (1đ):

Cho hàm số $y=f(x)$ có đồ thị của hàm số $y=f'(x)$ là đường cong như hình vẽ:

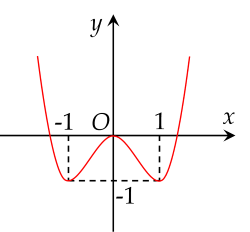
loading...

Hàm số $y=f(x)$ nghịch biến trên khoảng nào dưới đây?

(-\infty ;-\,1)

.

(1;\,+\infty)

.

(0;\,+\infty)

.

(-1;\,0)

.

Câu 8 (1đ):

Cho hàm số $y=f(x)$ có đồ thị $(C)$ như hình vẽ

Số nghiệm phân biệt của phương trình $f(x)=\dfrac{1}{2}$ là

1

.

0

.

3

.

2

.

Câu 9 (1đ):

Khảo sát thời gian chơi thể thao trong một ngày của 40 học sinh lớp 10A giáo viên thu được một mẫu dữ liệu ghép nhóm như sau:

Thời gian (phút)	Số học sinh
$[30;40)$	$2$
$[40;50)$	$10$
$[50;60)$	$16$
$[60;70)$	$8$
$[70;80)$	$2$
$[80;90)$	$2$

Khoảng tứ phân vị của bảng số liệu ghép nhóm trên là

\Delta_Q = 14,5

.

\Delta_Q = 14

.

\Delta_Q = 17,5

.

\Delta_Q = 17

.

Câu 10 (1đ):

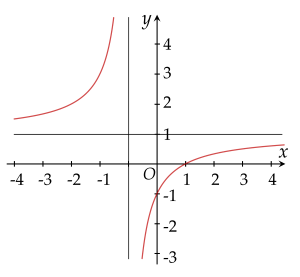
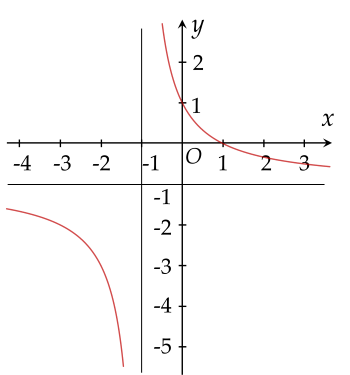
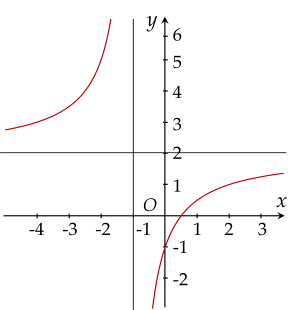
Đường cong nào sau đây là đồ thị của hàm số $y=\dfrac{1-x}{x+1}$ ?

Câu 11 (1đ):

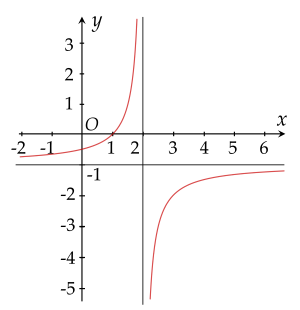
Tiệm cận xiên của đồ thị hàm số $y=\dfrac{-{{x}^{2}}-2x+5}{x+2}$ là

y=-x+1.

y=-x+3.

y=-x.

y=-x+2.

Câu 12 (1đ):

Để loại bỏ $x\%$ chất gây ô nhiễm không khí từ khí thải của một nhà máy, người ta ước tính chi phí cần bỏ ra là $C(x)=\dfrac{300x}{100-x}$ (triệu đồng), $0 \le x \le 100$ trong đó $C(x)$ là hàm số xác định trên $[ 0;100]$ . Đường tiệm cận đứng của đồ thị hàm số $y = C(x)$ là đường thẳng $x=x_0$ . Giá trị của $x_0$ là

-300

.

300

.

3

.

100

.

Câu 13 (1đ):

Cho hàm số $y=x^3+3x^2-9x+15$ .

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Tập xác định của hàm số là $(1;\,+\infty)$ .
b) Hàm số có đạo hàm là $y'=3x^2+6x-9$ .
c) Hàm số đồng biến trên khoảng $(-3;\,1)$ .
d) Đồ thị hàm số đạt cực trị tại $2$ điểm $A,\,B$ . Chu vi của tam giác $OAB$ bằng $3\sqrt{197}+4\sqrt{65}+\sqrt{101}$ (với $O$ là gốc tọa độ).

Câu 14 (1đ):

Cho hình hộp $ABCD.A'B'C'D'$ ; Các điểm $M,\,N$ lần lượt thuộc các đường thẳng $CA$ và $DC'$ sao cho $\overrightarrow{MC}=m\overrightarrow{MA};\,\,\overrightarrow{ND}=m\overrightarrow{NC'}$ . Đặt $\overrightarrow{BA}=\overrightarrow{a};\,\,\overrightarrow{BB'}=\overrightarrow{b};\,\overrightarrow{BC}=\overrightarrow{c}$ .

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) $\overrightarrow{BD'}=\overrightarrow{a}+\overrightarrow{b}-\overrightarrow{c}$ .
b) $\overrightarrow{BM}=\dfrac{\overrightarrow{c}-m\overrightarrow{a}}{1-m}$ .
c) $\overrightarrow{BN}=\dfrac{1}{1-m}\overrightarrow{a}-\dfrac{m}{1-m}\overrightarrow{b}+\overrightarrow{c}$ .
d) $m=\dfrac{1}{2}$ thì $MN$ // $BD'$ .

Câu 15 (1đ):

Giá đóng cửa của một cổ phiếu là giá của cổ phiếu đó cuối một phiên giao dịch. Bảng sau thống kê giá đóng cửa của hai mã cổ phiếu $A$ và $B$ trong $50$ ngày giao dịch liên tiếp.

Giá đóng cửa	Cổ phiếu $A$	Cổ phiếu $A$
$[120;122)$	$8$	$16$
$[122;124)$	$9$	$4$
$[124;126)$	$12$	$3$
$[126;128)$	$10$	$6$
$[128;130)$	$11$	$21$

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Xét mẫu số liệu của cổ phiếu $A$ ta có phương sai của mẫu số liệu ghép nhóm là $7,5216$ .
b) Xét mẫu số liệu của cổ phiếu $B$ ta có số trung bình của mẫu số liệu ghép nhóm là $115,28$ .
c) Xét mẫu số liệu của cổ phiếu $B$ ta có độ lệch chuẩn của mẫu số liệu ghép nhóm là $\sqrt{15,4096}$ .
d) Người ta có thể dùng phương sai và độ lệch chuẩn để so sánh mức độ rủi ro của các loại cổ phiếu có giá trị trung bình gần bằng nhau. Theo quan điểm trên, thì cổ phiếu $A$ có độ rủi ro thấp hơn cổ phiếu $B$ .

Câu 16 (1đ):

Số dân của một thị trấn sau $t$ năm kể từ năm $1\,970$ được ước tính bởi công thức $f(t)=\dfrac{26t+10}{t+5}$ (với $f(t)$ được tính bằng nghìn người). Coi $y=f(t)$ là một hàm số xác định trên nửa khoảng $[ 0;\,+\infty)$ .

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Dân số của thị trấn đó vào năm $2\,025$ là $34$ nghìn người.
b) Đạo hàm của hàm số luôn nhận giá trị âm trên khoảng $(0; +\infty)$ .
c) Đồ thị hàm số $y=f(t)$ có đường tiệm cận ngang là $y=26$ .
d) Dân số của thị trấn đó không thể vượt quá $26$ nghìn người.

Câu 17 (1đ):

Bảng dưới đây thống kê cự li ném tạ của một vận động viên.

Cự li (m)	Tần số
$[19;19,5)$	$12$
$[19,5;20)$	$46$
$[20;20,5)$	$20$
$[20,5;21)$	$16$
$[21;21,5)$	$6$

Tính phương sai của mẫu số liệu ghép nhóm trên. (Làm tròn kết quả đến chữ số hàng phần trăm).

Trả lời: .

Câu 18 (1đ):

Trong hóa học cấu tạo của phân tử ammoniac $(NH_3)$ có dạng hình chóp tam giác đều mà đỉnh là nguyên tử nitrogen $(N)$ và đáy là tam giác $H_1H_2H_3$ với $H_1,\,H_2,\,H_3$ là vị trí của ba nguyên tử hydrogen $(H)$ . Góc tạo bởi liên kết $H-N-H,$ có hai cạnh là hai đoạn thẳng nối $N$ với hai trong ba điểm $H_1,\,H_2,\,H_3$ (chẳng hạn như $\widehat{H_1NH_2}$ ) , được gọi là góc liên kết của phân tử $NH_3$ . Góc này xấp xỉ $120^{\circ }$ . Trong không gian $Oxyz,$ cho một phân tử $NH_3$ được biểu diễn bởi hình chóp tam giác đều $N.H_1H_2H_3$ với $O$ là tâm của đáy. Nguyên tử nitrogen được biểu diễn bởi điểm $N$ thuộc trục $Oz$ , ba nguyên tử hydrogen ở các vị trị $H_1,\,H_2,\,H_3$ trong đó $H_1\left( 0;-\sqrt{3};0 \right)$ và $H_2H_3$ song song với trục $Ox$ . Tính khoảng cách giữa nguyên tử nitrogen với mỗi nguyên tử hydrogen. (làm tròn kết quả đến hàng phần trăm)

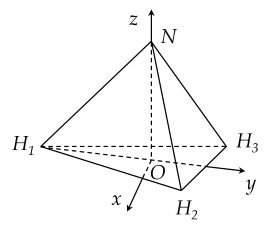
loading...

Trả lời:

Câu 19 (1đ):

Cho hình hộp $A B C D . A' B' C' D'$ có các cạnh đều bằng $a$ và $\widehat{B' A' D'}=60^{\circ}, \, \widehat{B' A' A}=\widehat{D' A' A}=120^{\circ}$ . Tính số đo (đơn vị độ) của góc giữa hai đường thẳng $A B$ với $A' D$ .

Trả lời:

Câu 20 (1đ):

Cho hàm số $y=\dfrac{m{{x}^{2}}+\left(m+2 \right)x+5}{{{x}^{2}}+1}$ . Gọi $S$ là tập hợp các giá trị của $m$ sao cho đồ thị hàm số đã cho có đúng hai điểm cực trị và đường thẳng nối hai điểm cực trị của đồ thị hàm số cắt hai trục tọa độ tạo thành một tam giác có diện tích bằng $\dfrac{25}{4}$ . Tính tổng giá trị các phần tử thuộc tập $S$ .

Trả lời:

Câu 21 (1đ):

Có bao nhiêu giá trị nguyên thuộc đoạn $[-2 \, 023;2 \, 023]$ của tham số thực $m$ để hàm số $y=\left| {\mathrm{e}^{3x}}-3(m+2){\mathrm{e}^{2x}}+3m(m+4){\mathrm{e}^{x}} \right|$ đồng biến trên khoảng $(-\infty ;\ln 2)$ ?

Trả lời:

Câu 22 (1đ):

Một con cá hồi bơi ngược dòng để vượt một khoảng cách là $300$ km. Vận tốc của dòng nước là $6$ km/h. Nếu vận tốc bơi của cá khi nước đứng yên là $v$ (km/h) thì năng lượng tiêu hao của cá trong $t$ giờ được cho bởi công thức: $E(v) = cv^3 t$ . Trong đó $c$ là một hằng số, $E$ được tính bằng jun. Tìm vận tốc bơi đơn vị km/h của cá khi nước đứng yên để năng lượng tiêu hao là ít nhất.

Trả lời:

Bài học cùng chủ đề

Đề kiểm tra học kì I (đề số 2) SVIP

Yêu cầu đăng nhập!

Bài học cùng chủ đề

Báo cáo học liệu

Mua học liệu

Mua học liệu:

Số dư ví của bạn: 0 coin - 0 Xu

Nếu mua học liệu này bạn sẽ bị trừ: 0 coin\Xu

Để nhận Coin\Xu, bạn có thể:

Chi tiết xem tại đây

Thông tin của bạn

Đề kiểm tra học kì I (đề số 2) SVIP

Yêu cầu đăng nhập!

Truy vết IP log

Báo lỗi câu hỏi

Các khóa học có thể bạn quan tâm

Yêu cầu VIP