Bài học cùng chủ đề
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 0 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Đề kiểm tra giữa học kì II (đề số 1) SVIP
Yêu cầu đăng nhập!
Bạn chưa đăng nhập. Hãy đăng nhập để làm bài thi tại đây!
Cho hàm số y=f(x) liên tục trên R và có một nguyên hàm là hàm số F(x), k∈N\{0}. Mệnh đề nào dưới đây sai?
Hàm số nào dưới đây là một nguyên hàm của hàm số f(x)=2x.3x?
Họ nguyên hàm của hàm số f(x)=4x5−x1+2025 là
Cho hàm số y=f(x) có đạo hàm liên tục trên [−2;3] thỏa mãn −2∫3f′(x)dx=8 và f(3)=12. Khi đó, f(−2) bằng
Trong không gian Oxyz, cho ba điểm A(3;0;0),B(0;−1;0),C(0;0;2). Mặt phẳng (α) đi qua A,B,C có phương trình là
Trong không gian Oxyz, cho hai mặt phẳng (P):x−2y−2z+1=0 và (Q):x−2y−2z+7=0. Khoảng cách giữa hai mặt phẳng (P) và (Q) bằng
Trong không gian Oxyz cho mặt phẳng (P):x−y+3=0. Vectơ nào sau đây không phải là vectơ pháp tuyến của mặt phẳng (P) ?
F(x) là một nguyên hàm của hàm số f(x)=ex−1 trên (−∞;+∞)/ Biết F(0)=2, hàm số F(x) là
Cho hàm số y=f(x) có đạo hàm f′(x)=cosx+1,∀x∈R. Biết 0∫2πf(x)dx=8π2+1, khi đó f(2π) bằng
Tích phân I=1∫2x+1−x1dx bằng
Trong không gian Oxyz, mặt phẳng đi qua gốc tọa độ và song song với mặt phẳng 5x−3y+2z−3=0 có phương trình là
Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC với A(1;−2;3), B(0;2;−1), C(3;0;−2). Phương trình mặt phẳng (P) đi qua A, trọng tâm G của tam giác ABC và vuông góc với (ABC) là
Cho (H) là hình phẳng giới hạn bởi 41 cung tròn có bán kính R=2, đường cong y=4−x và trục hoành, x=3.
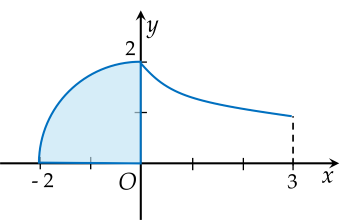
| a) Công thức tính diện tích hình quạt trên hình theo tích phân là −2∫04−x2dx |
|
| b) Diện tích hình phẳng (H) gần bằng 6,5. |
|
| c) Thể tích nửa khối cầu bán kính R=2 là 16π. |
|
| d) Thể tích V khối tạo thành khi cho (H) quay quanh Ox là 677π. |
|
Trong không gian với hệ trục toạ độ Oxyz, cho điểm A(1;2;5) và mặt phẳng (α):x+2y+2z−6=0.
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) Vectơ n=(1;2;2) là một vectơ pháp tuyến của (α). |
|
| b) Phương trình mặt phẳng (β) đi qua điểm A và song song với mặt phẳng (α) có phương trình x+2y+2z+15=0 |
|
| c) Phương trình mặt phẳng (γ) đi qua hai điểm O và A đồng thời vuông góc với mặt phẳng (α) có phương trình 2x−y=0. |
|
| d) Điểm M∈(α) sao cho A,O,M thẳng hàng thì tọa độ M(52;54;2). |
|
Một ô tô bắt đầu chuyển động nhanh dần đều với vận tốc v1(t)=4t m/s, trong đó thời gian t tính bằng giây. Sau khi chuyển động được 10 giây thì ô tô gặp chuớng ngại vật và người tài xế phanh gấp, ô tô tiếp tục chuyển động chậm dần đều với vận tốc v2(t) và gia tốc là a=−3 m/s2 cho đến khi dừng hẳn.
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) Quãng đường ô tô chuyển động nhanh dần đều là 200 m. |
|
| b) Vận tốc của ô tô tại thời điểm người tài xế phanh gấp là 40 m/s. |
|
| c) Thời gian từ lúc ô tô giảm tốc độ cho đến khi dừng hẳn là 40 giây. |
|
| d) Tổng quãng đường ô tô chuyển động từ lúc xuất phát đến khi dừng hẳn là khoảng 650,7 m. |
|
Một bác thợ xây bơm nước vào bể chứa nước. Gọi h(t) là thể tích nước bơm được sau t giây. Cho h′(t)=3at2+bt (m3/s) và ban đầu bể không có nước. Sau 5 giây thì thể tích nước trong bể là 150 m3. Sau 10 giây thì thể tích nước trong bể là 1100 m3. Thể tích nước trong bể sau khi bơm được 20 giây là bao nhiêu m3? (Làm tròn kết quả đến chữ số hàng đơn vị)
Trả lời:
Một viên đạn được bắn lên theo phương thẳng đứng với vận tốc ban đầu là 25 m/s, gia tốc trọng trường là 9,8 m/s2. Quãng đường viên đạn đi được từ lúc bắn cho đến khi chạm đất là bao nhiêu mét? (Làm tròn kết quả đến chữ số thập phân thứ nhất)
Trả lời:
Một vật chuyển động trong 3 giờ với vận tốc v (km/h) phụ thuộc thời gian t (h) có đồ thị là một phần của đường parabol có đỉnh I(2;9) và trục đối xứng song song với trục tung như hình bên. Tính quãng đường s (km) mà vật di chuyển được trong 3 giờ đó.
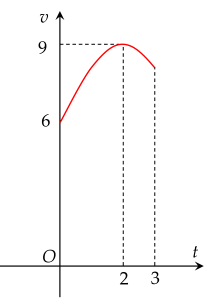
Trả lời:
Trong không gian Oxyz, cho mặt phẳng (α):2x+3y+z+1=0. Gọi (P) là mặt phẳng song song với (α), cắt các tia Ox,Oy,Oz lần lượt tại các điểm A, B, C sao cho thể tích khối tứ diện OABC bằng 6. Tính khoảng cách từ gốc tọa độ O đến mặt phẳng (P) (kết quả làm tròn đến hàng phần mười).
Trả lời:
Một người có mảnh đất hình tròn có bán kính 5 m, người này tính trồng cây trên mảnh đất đó, biết mỗi mét vuông trồng cây thu hoạch được giá 100 nghìn đồng. Tuy nhiên cần có khoảng trống để dựng chòi và đồ dùng nên người này căng sợi dây 6 m sao cho hai đầu mút dây nằm trên đường tròn xung quanh mảnh đất. Người này thu hoạch được bao nhiêu tiền (tính theo đơn vị nghìn đồng)?
Trả lời: nghìn đồng.
Trong không gian với hệ trục tọa độ Oxyz. Phương trình mặt phẳng (P) đi qua hai điểm A(1;1;1),B(0;2;2) đồng thời cắt các tia Ox,Oy lần lượt tại các điểm M,N (M,N không trùng với gốc tọa độ O) thỏa mãn OM=2ON là ax+by+cz+d=0. Tính T=a+b+c+d.
Trả lời:
