Bài học cùng chủ đề
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 0 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Đề kiểm tra giữa học kì II (đề số 1) SVIP
Yêu cầu đăng nhập!
Bạn chưa đăng nhập. Hãy đăng nhập để làm bài thi tại đây!
Kí hiệu K là một khoảng hoặc nửa khoảng hoặc một đoạn của R. Mệnh đề nào sau đây sai?
Họ các nguyên hàm của hàm số f(x)=4x3−2x2+1 là
Họ các nguyên hàm ∫2x+11dx là
Cho 2∫3f(x)dx=2; 2∫3g(x)dx=−3. Giá trị của A=2∫3[3f(x)−2g(x)]dx là
Cho hàm số y=f(x) và y=g(x) có đồ thị như hình vẽ:
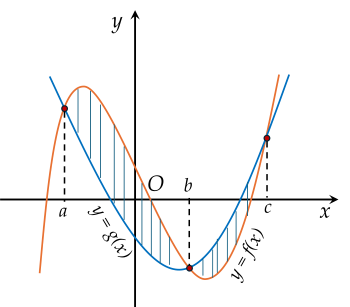
Diện tích S của phần gạch chéo trong hình vẽ trên được tính bằng công thức là
Trong không gian Oxyz, mặt phẳng (α):2x+3y+−5z=1 có vectơ pháp tuyến là
Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm A(1;0;0),B(0;−2;0). Phương trình mặt phẳng (OAB) là
Gọi là các số nguyên sao cho 0∫2ex+2dx=2ae2+be. Giá trị của a2+b2 bằng
Tích phân a∫b(1+sinx)dx với a<b có giá trị là
Cho hình phẳng (H) giới hạn bởi đồ thị hàm số y=−x, đường thẳng y=−x+2 và trục hoành.
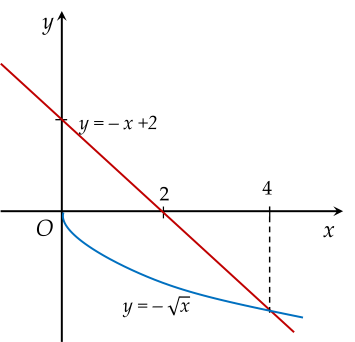
Khối tròn xoay tạo ra khi (H) quay quanh Ox có thể tích V được xác định bằng công thức nào sau đây?
Trong không gian Oxyz, hai mặt phẳng (P): x+2y−2z+3=0 và (Q): −x−2y+2z−12=0 lần lượt chứa hai mặt bên của một hình lập phương. Thể tích khối lập phương đó là
Biết F(x) là một nguyên hàm của hàm số f(x)=x2. Biểu thức F′(25) bằng
Cho hàm số F(x)=x3−2x+1, x∈R là một nguyên hàm của hàm số f(x).
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) Nếu hàm số G(x) cũng là một nguyên hàm của hàm số f(x) và G(−1)=3 thì G(x)=F(x)−1, x∈R. |
|
| b) Nếu hàm số H(x) cũng là một nguyên hàm của hàm số f(x) và H(1)=−3 thì H(x)=F(x)−3, x∈R. |
|
| c) Nếu hàm số K(x) cũng là một nguyên hàm của hàm số f(x) và K(0)=0 thì K(x)=F(x)+1, x∈R. |
|
| d) Nếu hàm số M(x) cũng là một nguyên hàm của hàm số f(x) và M(2)=4 thì M(x)=F(x)−1, x∈R. |
|
Cho hàm số y=f(x) liên tục trên đoạn [0;8] và có đồ thị như hình vẽ:
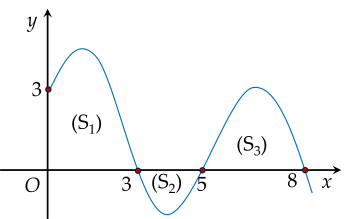
| a) S1=∫03f(x)dx. |
|
| b) S2+S3=∫38f(x)dx. |
|
| c) S1−S2=−∫05f(x)dx. |
|
| d) ∫08f(x)dx>∫58f(x)dx. |
|
Mặt phẳng (α) là mặt phẳng đi qua điểm A(1;2;−3) và vuông góc với hai mặt phẳng: (P): x+y+z+2=0; (Q): 2x−y+z−4=0.
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) Mặt phẳng (α) có một vectơ pháp tuyến là: n=(−2;1;3) |
|
| b) Mặt phẳng (α) có phương trình là: 2x+y−3z−13=0 |
|
| c) Mặt phẳng (α) đi qua điểm B(2;0;0) |
|
| d) Mặt phẳng (α) song song với mặt phẳng (β): 4x+2y−6z−3=0 |
|
Trong hệ trục tọa độ cho các điểm M(0;2;0),N(0;0;−1),P(−1;0;3).
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) Trọng tâm tam giác MNP là điểm G(0;2;1). |
|
| b) Điểm M thuộc mặt phẳng (α):2x+y−2z=0. |
|
| c) Diện tích tam giác OMN=1. |
|
| d) Tồn tại 2 mặt phẳng (α) qua hai điểm M, N và có khoảng cách từ P đến (α) bằng 2. |
|
Chủ một trung tâm thương mại muốn cho thuê một số gian hàng như nhau. Người đó muốn tăng giá cho thuê của mỗi gian hàng thêm x (triệu đồng), (x≥0). Tốc độ thay đổi doanh thu từ các gian hàng đó được biểu diễn bởi hàm số T′(x)=−20x+300, trong đó T′(x) tính bằng triệu đồng. Biết rằng nếu người đó tăng giá thuê cho mỗi gian hàng thêm 10 triệu đồng thì doanh thu là 12000 triệu đồng. Giá trị của x bằng bao nhiêu để người đó có doanh thu là cao nhất?
Trả lời:
Một vật chuyển động trong 3 giờ với vận tốc v (km/h) phụ thuộc thời gian t (h) có đồ thị là một phần của đường parabol có đỉnh I(2;9) và trục đối xứng song song với trục tung như hình bên. Tính quãng đường s (km) mà vật di chuyển được trong 3 giờ đó.
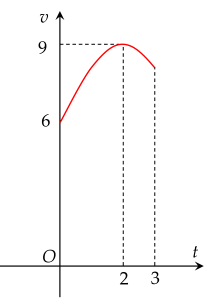
Trả lời:
Một khối cầu có bán kính là 5 dm, người ta cắt bỏ hai phần của khối cầu bằng hai mặt phẳng song song cùng vuông góc đường kính và cách tâm một khoảng 3 dm để làm một chiếc lu đựng nước. Thể tích của chiếc lu bằng bao nhiêu? (làm tròn đến hàng đơn vị).
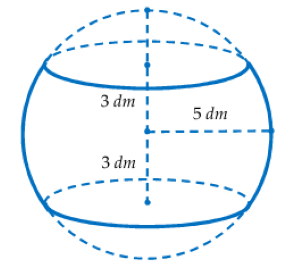
Trả lời: dm3.
Cho hình phẳng (H) được giới hạn bởi đường cong y=m2−x2 (m là tham số khác 0) và trục hoành. Khi (H) quay xung quanh trục hoành được khối tròn xoay có thể tích V. Có bao nhiêu giá trị nguyên của m để V<1000π?
Trả lời:
Trong không gian Oxyz, cho điểm M(1;3;−1) và mặt phẳng (P):x−2y+2z=1. Gọi N là hình chiếu vuông góc của M trên (P). Phương trình mặt phẳng trung trực của đoạn MN có dạng Ax+By+Cz+D=0, trong đó A,B,C,D∈Z và 0<D<5. Tổng A+B+C+D bằng bao nhiêu?
Trả lời:
Trong không gian Oxyz, cho điểm A(1011;1;0) và mặt phẳng (Q):x−y−7z+2=0. Biết (P) // (Q) và (P) có dạng x+by+cz+m=0. Tính ∣T∣, với T tổng các giá trị của m sao cho d(A;(P))=1.
Trả lời:
