Bài học cùng chủ đề
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 0 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Đề kiểm tra giữa học kì I (đề số 3) SVIP
Yêu cầu đăng nhập!
Bạn chưa đăng nhập. Hãy đăng nhập để làm bài thi tại đây!
Hàm số y=x3−2x2+x+1 nghịch biến trên khoảng nào dưới đây?
Cho hàm số y=f(x) xác định, liên tục trên R và có bảng xét dấu đạo hàm như hình vẽ.

Hàm số y=f(x) có bao nhiêu điểm cực trị?
Cho hàm số y=f(x) xác định trên R, có đồ thị như hình vẽ. Mệnh đề nào sau đây đúng?
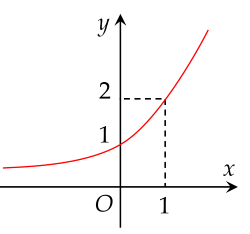
Giá trị nhỏ nhất của hàm số y=x+x9 trên đoạn [2;4] là
Đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y=x+12x−3 là
Đồ thị hàm số nào sau đây có đồ thị như hình vẽ?

Đồ thị hàm số y=2x−12x+1 có tọa độ giao điểm với trục tung là
Cho hàm số y=x−22x−3 có đồ thị là (C). Tiếp tuyến của đồ thị cắt tiệm cận đứng và tiệm cận ngang lần lượt tại A,B sao cho côsin góc ABI bằng 174, với I(2;2). Khi đó, phương trình tiếp tuyến của đồ thị hàm số có dạng
Đồ thị hàm số y=−x+2x−1 nhận điểm nào dưới đây là tâm đối xứng?
Một bể chứa 1000 lít nước muối có nồng độ 0,1 (tính bằng tỉ số của khối lượng muối trong bể và thể tích bể, đơn vị gam/lít). Người ta bơm nước muối có nồng độ 0,2 vào bể với tốc độ 20 lít/phút. Gọi f(t) là nồng độ muối trong bể sau t phút. Tiệm cận ngang của đồ thị hàm số y=f(t) là đường thẳng
Với giá trị nào dưới đây của m thì hàm số y=cos2x+mx đồng biến trên R?
Có tất cả bao nhiêu giá trị khác nhau của tham số m để đồ thị hàm số y=x2+mx+4x−1 có hai đường tiệm cận?
Cho hàm số y=f(x) liên tục và có đồ thị trên đoạn [−2;4] như hình vẽ.
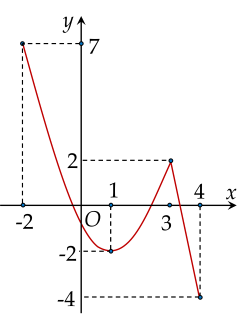
| a) Trên đoạn [−2;4], đồ thị hàm số y=f(x) có 2 điểm cực trị. |
|
| b) Giá trị nhỏ nhất của hàm số y=f(x) trên đoạn [−2;2] là −2. |
|
| c) Giá trị lớn nhất của hàm số y=f(x) trên đoạn [1;4] là −4. |
|
| d) Hiệu giữa giá trị lớn nhất và giá trị nhỏ nhất của hàm số y=f(x) trên đoạn [−2;4] là 11. |
|
Cho hàm số y=2x−11−4x có đồ thị (C).
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) Đồ thị (C) có tiệm cận ngang là đường thẳng y=2. |
|
| b) Đồ thị (C) có tiệm cận đứng là y=21. |
|
| c) Đường tiệm cận ngang cắt đồ thị hàm số y=x3−3x−2 tại 3 điểm. |
|
| d) Hình chữ nhật giới hạn bởi 2 tiệm cận của đồ thị và hai trục tọa độ có diện tích bằng 1. |
|
Một loại thuốc được dùng cho một bệnh nhân và nồng độ thuốc trong máu của bệnh nhân được giám sát bởi bác sĩ. Biết rằng nồng độ thuốc trong máu của bệnh nhân sau khi tiêm vào cơ thể trong t giờ được cho bởi hàm số có công thức c(t)=t2+1t (mg/L).
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) Nồng độ thuốc trong máu của bệnh nhân sau 3 giờ là c(3)=103 (mg/L). |
|
| b) Đạo hàm của hàm số c(t)=t2+1t là c′(t)=(t2+1)21−t2. |
|
| c) Nồng độ thuốc trong máu bệnh nhân tăng trong khoảng t∈(0;2). |
|
| d) Nồng độ thuốc trong máu của bệnh nhân cao nhất khi t=21. |
|
Cho hàm số y=x−3x+1.
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) Hàm số đồng biến trên (−∞;3). |
|
| b) Hàm số có tiệm cận ngang y=1. |
|
| c) Tỉ số giữa GTLN và GTNN của hàm số y=x−3x+1 trên [4;7] là 45. |
|
| d) Đường thẳng y=x−m cắt y=x−3x+1 tại 2 điểm phân biệt ∀m∈R. |
|
Một bể chứa 2 m3 nước tinh khiết. Người ta bơm vào bể đó nước muối có nồng độ không đổi với tốc độ 20 lít/phút. Biết rằng nồng độ muối trong bể sau t phút (tính bằng tỉ số của khối lượng muối trong bể và thể tích nước trong bể, đơn vị: gam/lít) là một hàm số f(t), thời gian t tính bằng phút. Biết rằng tiệm cận ngang của đồ thị hàm số y=f(t) là y=10. Tính nồng độ muối trong bể sau khi bơm được 1 giờ. (làm tròn kết quả đến hàng phần trăm, đơn vị gam/lít)
Trả lời:
Giả sử doanh số (tính bằng số sản phẩm) của một sản phẩm mới (trong vòng một số năm nhất định) tuân theo quy luật logistic được mô hình hoá bằng hàm số y=f(t)=1+5e−t5000,t≥0, trong đó thời gian t (năm) được tính kể từ khi phát hành sản phẩm mới. Khi đó, đạo hàm f′(t) sẽ biểu thị tốc độ bán hàng. Sau khi phát hành bao nhiêu năm thì tốc độ bán hàng là lớn nhất? (làm tròn kết quả tới chữ số hàng phần mười)
Trả lời:
Độ giảm huyết áp của một bệnh nhân được xác định bởi công thức G(x)=0,024x2(30−x), trong đó x là liều lượng thuốc tiêm cho bệnh nhân cao huyết áp (x được tính bằng mg). Tìm lượng thuốc x tiêm cho bệnh nhân cao huyết áp để huyết áp giảm nhiều nhất.
Trả lời:
Một chất điểm chuyển động theo quy luật và quãng đường di chuyển được sau t giây được tính theo công thức S(t)=−3t3+243t2 (m). Vận tốc v (m/s) của chuyển động đạt giá trị lớn nhất khi t bằng bao nhiêu giây?
Trả lời:
Cho hàm số y=f(x) có đạo hàm trên R. Biết rằng hàm số y=f′(x) có đồ thị như hình vẽ bên dưới.
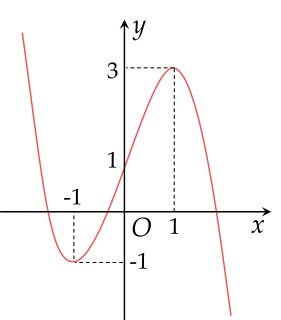
Đồ thị hàm số y=f(3x−2) cắt đường thẳng y=2x−3 tại nhiều nhất bao nhiêu điểm?
Trả lời:
Cho hàm số y=f(x) có đạo hàm f′(x)=x2(x−9)(x−4)2. Khi đó hàm số g(x)=f(x2) nghịch biến trên khoảng (0;k) với k là số nguyên. Giá trị của k là bao nhiêu?
Trả lời:
