Đề kiểm tra giữa học kì I toán 12 cấu trúc mới mới nhất

Câu 1 (1đ):

Trong không gian cho ba điểm $M,\,N,\,P$ phân biệt. Tổng $\overrightarrow{PM}+\overrightarrow{MN}$ là

\overrightarrow{MN}

.

\overrightarrow{NP}

.

\overrightarrow{NM}

.

\overrightarrow{PN}

.

Câu 2 (1đ):

Trong không gian $Oxyz$ , biết $\overrightarrow{OM}=2\overrightarrow{i}-3\overrightarrow{j}+\overrightarrow{k}$ . Toạ độ của điểm $M$ là

(2;1;-3)

.

(-3;2;1)

.

(2;-3;1)

.

(-2;3;-1)

.

Câu 3 (1đ):

Cho hàm số $y=f(x)$ có đạo hàm $f'(x)=(x-1)(2-x)$ , $\forall x\in \mathbb{R}$ . Điểm cực đại của hàm số là

y=1

.

y=-2

.

x=2

.

x=-1

.

Câu 4 (1đ):

Cho hàm số $y=f(x)$ có đồ thị là đường cong như hình vẽ:

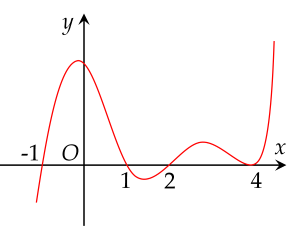
loading...

Hàm số đã cho nghịch biến trên khoảng nào dưới đây?

(-\infty ;\,-1)

.

(0;\,1)

.

(1;\,2)

.

(-1;\,1).

Câu 5 (1đ):

Giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y = f\left( x \right)=\dfrac{8}{1+2x}+x$ trên đoạn $\left[ 1;2 \right]$ lần lượt là

\dfrac{11}{3}

;

\dfrac{7}{2}

.

\dfrac{18}{5}

;

\dfrac{3}{2}

.

\dfrac{11}{3}

;

\dfrac{18}{5}

.

\dfrac{13}{3}

;

\dfrac{7}{2}

.

Câu 6 (1đ):

Đồ thị hàm số nào sau đây có hình dạng như hình vẽ bên?

y=-x^3+3x+1

.

y=-x^3+3x^2-4

.

y=x^4-x^2-4

.

y=x^3-3x+1

.

Câu 7 (1đ):

Đồ thị hàm số $y=\dfrac{x-1}{-x+2}$ nhận điểm nào dưới đây là tâm đối xứng?

B(-2;1)

.

C(2;1)

.

A(-2;-1)

.

D(2;-1)

.

Câu 8 (1đ):

Đồ thị hàm số nào sau đây cắt trục tung tại điểm có tung độ âm?

y=\dfrac{4x+1}{x+2}

.

y=\dfrac{-2x+3}{x+1}

.

y=\dfrac{2x-3}{3x-1}

.

y=\dfrac{3x+4}{x-1}

.

Câu 9 (1đ):

Một ứng dụng của hàm số trong vật lí là hệ số tương đối tính Lorentz được cho bởi công thức $\gamma (v)=\dfrac{1}{\sqrt{1-\dfrac{v^2}{c^2}}}$ , với $v$ là vận tốc tương đối giữa các hệ quy chiếu quán tính, $c$ là tốc độ ánh sáng trong chân không. Hàm này được sử dụng trong thuyết tương đối đặc biệt của Einstein để mô tả các hiệu ứng tương đối tính có đồ thị dưới đây:

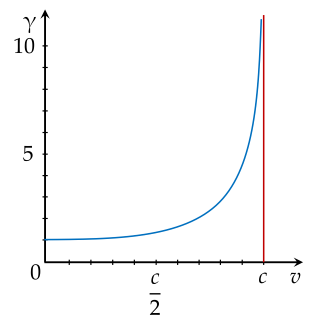
loading...

Đồ thị hàm số đó có tiệm cận đứng là

x=0

.

y=0

.

x=c

.

x=\dfrac{c}{2}

.

Câu 10 (1đ):

Cho hình lăng trụ $ABC.A'B'C'$ . Gọi $M$ là trung điểm của cạnh $BB'$ . Đặt $\overrightarrow{CA}=\overrightarrow{a}$ , $\overrightarrow{CB}=\overrightarrow{b}$ , $\overrightarrow{AA'}=\overrightarrow{c}$ . Khẳng định nào sau đây đúng?

\overrightarrow{AM}=\overrightarrow{a}-\overrightarrow{c}+\dfrac{1}{2}\overrightarrow{b}

.

\overrightarrow{AM}=\overrightarrow{b}+\overrightarrow{c}-\dfrac{1}{2}\overrightarrow{a}

.

\overrightarrow{AM}=\overrightarrow{b}-\overrightarrow{a}+\dfrac{1}{2}\overrightarrow{c}

.

\overrightarrow{AM}=\overrightarrow{a}+\overrightarrow{c}-\dfrac{1}{2}\overrightarrow{b}

.

Câu 11 (1đ):

Trong không gian với hệ trục tọa độ $O x y z$ , cho tam giác $A B C$ có ba đỉnh $A(-1 ; 1 ;-3)$ , $B (4 ; 2 ; 1)$ , $C( 3 ; 0 ; 5)$ . Tọa độ trọng tâm $G$ của tam giác $A B C$ là

G (2 ; 1 ; 1).

G (3 ; 1 ; 1).

G (1 ; 3 ; 2).

G(-1 ; 2 ; 1).

Câu 12 (1đ):

Cho hình lăng trụ $ABC.A'B'C'$ . Đặt $\overrightarrow{AA'}=\overrightarrow{a}$ , $\overrightarrow{AB}=\overrightarrow{b}$ , $\overrightarrow{AC}=\overrightarrow{c}$ . Biểu diễn vectơ $\overrightarrow{B'C}$ theo $\overrightarrow{a},\,\overrightarrow{b},\,\overrightarrow{c}$ được

\overrightarrow{B'C}=-\overrightarrow{a}+\overrightarrow{b}-\overrightarrow{c}

.

\overrightarrow{B'C}=-\overrightarrow{a}-\overrightarrow{b}+\overrightarrow{c}

.

\overrightarrow{B'C}=\overrightarrow{a}+\overrightarrow{b}-\overrightarrow{c}

.

\overrightarrow{B'C}=\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}

.

Câu 13 (1đ):

Cho hình hộp $ABCD.{A}'{B}'{C}'{D}'$ .

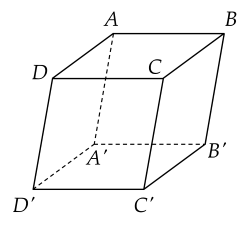
loading...

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) $\overrightarrow{AB}=\overrightarrow{D'C'}$ .
b) $\overrightarrow{AC'}=\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{AA'}$ .
c) $\overrightarrow{AB}+\overrightarrow{AA'}=\overrightarrow{AD}+\overrightarrow{DD'}.$
d) $\overrightarrow{AD}+\overrightarrow{DC}+\overrightarrow{CC'}=\overrightarrow{AD'}+\overrightarrow{D'C'}$ .

Câu 14 (1đ):

Cho hàm số $y=f(x)$ xác định, liên tục trên $\mathbb{R}$ và có bảng biến thiên:

(Nhấp vào ô màu vàng để chọn đúng / sai)

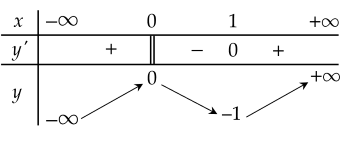
a) Hàm số có giá trị cực tiểu bằng $1$ .
b) Hàm số có giá trị lớn nhất bằng $0$ và giá trị nhỏ nhất bằng $-1$ .
c) Hàm số đạt cực đại tại $x=0$ và đạt cực tiểu tại $x=1$ .
d) Hàm số có đúng một cực trị.

Câu 15 (1đ):

Cho hàm số $y=f(x )=\dfrac{2x^2+3x-5}{x+3}$ có đồ thị $(C )$ , biết đồ thị có tiệm cận xiên là đường thẳng $\Delta:y=ax+b$ .

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Giao điểm của $\Delta$ và trục $Ox$ có hoành độ lớn hơn $2$ .
b) Giao điểm của $\Delta$ và tiệm cận đứng của $(C )$ có tọa độ là $(-3;-9 )$ .
c) Gọi $A=\Delta\cap Ox$ , $B=\Delta\cap Oy$ ta có $S_{OAB}>3$ .
d) Giá trị lớn nhất của hàm số $y=ax+b$ trên $[ 0;3]$ là $4$ .

Câu 16 (1đ):

Chi phí nhiên liệu của một chiếc tàu chạy trên sông được chia làm hai phần. Phần thứ nhất không phụ thuộc vào vận tốc và bằng $480$ nghìn đồng mỗi giờ. Phần thứ hai tỉ lệ thuận với lập phương của vận tốc, khi $v=10$ km/h thì phần thứ hai bằng 30 nghìn đồng mỗi giờ.

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Khi vận tốc $v=10$ (km/h) thì chi phí nguyên liệu cho phần thứ nhất trên mỗi km đường sông là $48\,000$ đồng.
b) Hàm số xác định tổng chi phí nguyên liệu trên mỗi km đường sông với vận tốc $x$ km/h là $f(x)=\dfrac{480}{x}+0,03 x^{3}$ .
c) Khi vận tốc $v=30$ km/h thì tổng chi phí nguyên liệu trên mỗi km đường sông là $43\,000$ đồng.
d) Vận tốc của tàu để tổng chi phí nguyên liệu trên mỗi km đường sông nhỏ nhất là $v=20$ km/h.

Câu 17 (1đ):

Có ba lực cùng tác động vào một vật. Hai trong ba lực này hợp với nhau một góc $100^\circ$ và có độ lớn lần lượt là $25$ N và $12$ N. Lực thứ ba vuông góc với mặt phẳng tạo bởi hai lực đã cho và có độ lớn $4$ N. Tính độ lớn của hợp lực của ba lực trên. (làm tròn đến hàng đơn vị)

Trả lời:

Câu 18 (1đ):

Trong không gian, cho hình hộp $ABCD.A'B'C'D'$ . Biết $\overrightarrow{MA}=k.\overrightarrow{MC}$ , $\overrightarrow{NC'}=l.\overrightarrow{ND}$ . Khi $MN$ song song với $BD'$ thì $k+l$ có giá trị là bao nhiêu?

Trả lời:

Câu 19 (1đ):

Một khách sạn có $80$ phòng cho thuê. Người quản lí của khách sạn nhận thấy rằng tất cả các phòng của khách sạn sẽ có người thuê hết nếu giá thuê một phòng là $700 \, 000$ đồng một ngày. Một cuộc khảo sát thị trường cho thấy rằng, trung bình cứ mỗi lần tăng giá thuê phòng thêm $50\,000$ đồng thì sẽ có thêm $2$ phòng bị bỏ trống. Người quản lí nên đặt giá thuê mỗi phòng một ngày là bao nhiêu triệu đồng để doanh thu là lớn nhất? Làm tròn kết quả đến chữ số thập phân thứ hai

Trả lời:

Câu 20 (1đ):

Cho hàm số $y=f(x)$ liên tục trên $\mathbb{R}$ , có đồ thị $(C )$ như hình vẽ sau:

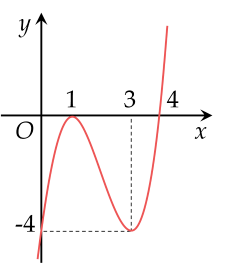
loading...

Phương trình $| f(x) |=2$ có bao nhiêu nghiệm trên đoạn $[ 0;3 ]$ ?

Trả lời:

Câu 21 (1đ):

Tại một công ty sản xuất đồ chơi an toàn cho trẻ em, công ty phải chi $40\,000$ USD để thiết lập dây chuyền sản xuất ban đầu. Sau đó, cứ sản xuất được một sản phẩm đồ chơi $A$ , công ty phải trả $6$ USD cho nguyên liệu ban đầu và nhân công. Gọi $x$ , ( $x \ge 1$ ) là số đồ chơi $A$ mà công ty đã sản xuất và $P(x)$ (đơn vị USD) là tổng số tiền bao gồm cả chi phí ban đầu mà công ty phải chi trả khi sản xuất $x$ đồ chơi $A$ . Người ta xác định chi phí trung bình cho mỗi sản phẩm đồ chơi $A$ là $F(x)=\dfrac{P(x)}{x}$ . Xem $y = F(x)$ là hàm số theo $x$ xác định trên nửa khoảng $\left[ 1;+\infty \right)$ có phương trình đường tiệm cận ngang là $y = b$ . Tính $b$ .

Trả lời:

Câu 22 (1đ):

Tìm giá trị nguyên lớn nhất của tham số $m$ để hàm số $y=\dfrac{x^2+(m-1)x+3-2m}{x+m}$ đạt cực tiểu tại $x=-1$ .

Trả lời:

Bài học cùng chủ đề

Đề kiểm tra giữa học kì I (đề số 2) SVIP

Yêu cầu đăng nhập!

Bài học cùng chủ đề

Báo cáo học liệu

Mua học liệu

Mua học liệu:

Số dư ví của bạn: 0 coin - 0 Xu

Nếu mua học liệu này bạn sẽ bị trừ: 0 coin\Xu

Để nhận Coin\Xu, bạn có thể:

Chi tiết xem tại đây

Thông tin của bạn

Đề kiểm tra giữa học kì I (đề số 2) SVIP

Yêu cầu đăng nhập!

Truy vết IP log

Báo lỗi câu hỏi

Các khóa học có thể bạn quan tâm

Yêu cầu VIP