Bài học cùng chủ đề
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 0 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Đề kiểm tra giữa học kì I (đề số 2) SVIP

Cho hàm số y=f(x) có đồ thị hàm số như hình vẽ:

Hàm số đã cho đồng biến trên khoảng nào dưới đây?
Hàm số y=−x4+8x2−7 có bao nhiêu điểm cực đại?
Gọi M,m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số y=5−4x trên đoạn [−1;1]. Giá trị M−m bằng
Cho hàm số bậc ba y=f(x) có đồ thị như hình vẽ:
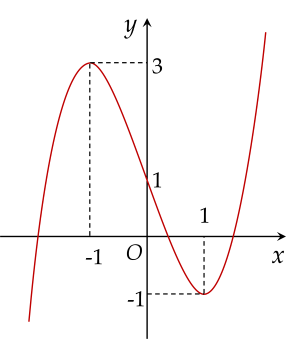
Trên đoạn [0;1], hàm số y=f(x) đạt giá trị nhỏ nhất tại
Đường tiệm cận xiên của đồ thị hàm số y=x+12x2−x+2 có phương trình là
Số điểm có tọa độ là các số nguyên thuộc đồ thị hàm số y=x+2x+3 là
Trong không gian với hệ tọa độ Oxyz, cho u=2i+3j−k, khi đó tọa độ vectơ u là
Cho hàm số y=cx+1ax+b (a,b,c∈R) có bảng biến thiên như sau:

Tập các giá trị b là tập nghiệm của bất phương trình nào dưới đây?
Cho hàm số y=x+12x−1 có đồ thị (C) và đường thẳng d:y=2x−3. Đường thẳng d cắt (C) tại hai điểm A và B. Khoảng cách giữa A và B là
Trong không gian với hệ trục tọa độ Oxyz, cho tam giác ABC có ba đỉnh A(−1;1;−3), B(4;2;1), C(3;0;5). Tọa độ trọng tâm G của tam giác ABC là
Cho hình lăng trụ ABC.A′B′C′. Đặt AA′=a, AB=b, AC=c. Biểu diễn vectơ B′C theo a,b,c được
Cho hàm số f(x)=bx+cax−2 (a,b,c∈R) có bảng biến thiên như sau.

Biểu thức T=2a+b−3c nhận được bao nhiêu giá trị nguyên?
Cho hàm số y=f(x) có bảng biến thiên như hình vẽ:
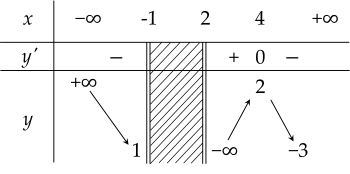
| a) Đồ thị hàm số có đường tiệm cận đứng x=2. |
|
| b) Hàm số có đúng 1 điểm cực trị. |
|
| c) Hàm số đạt giá trị lớn nhất là 2 tại x=4. |
|
| d) Hàm số đồng biến trên khoảng (2;3). |
|
Số dân của một thị trấn sau t năm kể từ năm 1970 được ước tính bởi công thức f(t)=t+526t+10 (với f(t) được tính bằng nghìn người). Coi y=f(t) là một hàm số xác định trên nửa khoảng [0;+∞).
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) Dân số của thị trấn đó vào năm 2025 là 34 nghìn người. |
|
| b) Đạo hàm của hàm số luôn nhận giá trị âm trên khoảng (0;+∞). |
|
| c) Đồ thị hàm số y=f(t) có đường tiệm cận ngang là y=26. |
|
| d) Dân số của thị trấn đó không thể vượt quá 26 nghìn người. |
|
Một loại thuốc được dùng cho một bệnh nhân và nồng độ thuốc trong máu của bệnh nhân được giám sát bởi bác sĩ. Biết rằng nồng độ thuốc trong máu của bệnh nhân sau khi tiêm vào cơ thể trong t giờ được cho bởi hàm số có công thức c(t)=t2+1t (mg/L).
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) Nồng độ thuốc trong máu của bệnh nhân sau 3 giờ là c(3)=103 (mg/L). |
|
| b) Đạo hàm của hàm số c(t)=t2+1t là c′(t)=(t2+1)21−t2. |
|
| c) Nồng độ thuốc trong máu bệnh nhân tăng trong khoảng t∈(0;2). |
|
| d) Nồng độ thuốc trong máu của bệnh nhân cao nhất khi t=21. |
|
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh đều bằng a. Gọi O là giao điểm của AC và BD.
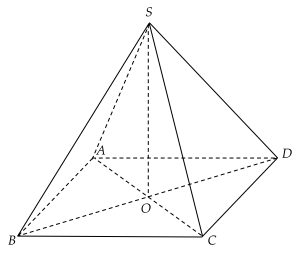
| a) OA+OB+OC+OD=0. |
|
| b) SA+SB+SC+SD=0. |
|
| c) AB.SO=0. |
|
| d) AB.BD=a2. |
|
Người ta muốn làm một cái bể dạng hình hộp chữ nhật không nắp (như hình vẽ) có thể tích bằng 1 m3. Chiều cao của bể là 5dm, các kích thước khác là x m, y m với x>0 và y>0. Diện tích toàn phần của bể (không kể nắp) là hàm số S(x) trên khoảng (0;+∞).
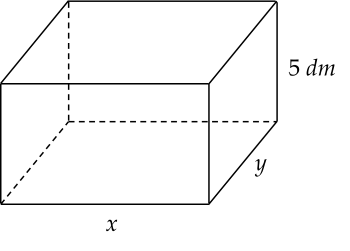
Đường tiệm cận xiên của đồ thị hàm số S(x) là đường thẳng y=ax+b. Tính P=a2+b2.
Trả lời:
Độ cao so với mặt đất của một quả bóng được ném lên theo phương thẳng đứng được mô tả bởi hàm số bậc hai h(t)=−4,9t2+20t+1, trong đó độ cao h(t) tính bằng mét và thời gian t tính bằng giây. Tại thời điểm x giây kể từ khi bắt đầu được ném lên thì quả bóng đạt độ cao lớn nhất. Tính x. (kết quả làm tròn đến hàng phần trăm)
Trả lời:
Độ giảm huyết áp của một bệnh nhân được xác định bởi công thức G(x)=0,024x2(30−x), trong đó x là liều lượng thuốc tiêm cho bệnh nhân cao huyết áp (x được tính bằng mg). Tìm lượng thuốc x tiêm cho bệnh nhân cao huyết áp để huyết áp giảm nhiều nhất.
Trả lời:
Một xí nghiệp A chuyên cung cấp sản phẩm S cho nhà phân phối B. Hai bên thỏa thuận rằng, nếu đầu tháng B đặt hàng x tạ sản phẩm S thì giá bán mỗi tạ sản phẩm S là P(x)=6−0,0005x2 (triệu đồng) (x≤40). Chi phí A phải bỏ ra cho x tạ sản phẩm S trong một tháng là C(x)=10+3,5x (triệu đồng) và mỗi sản phẩm bán ra phải chịu thêm mức thuế là 1 triệu đồng. Trong một tháng B cần đặt hàng bao nhiêu tạ sản phẩm S thì A có được lợi nhuận lớn nhất, kết quả làm tròn đến hàng phần mười.
Trả lời:
Ba chiếc máy bay không người lái cùng bay lên tại một địa điểm. Sau một thời gian bay, chiếc máy bay thứ nhất cách điểm xuất phát về phía Đông 60 (km) và về phía Nam 40 (km), đồng thời cách mặt đất 2 (km). Chiếc máy bay thứ hai cách điểm xuất phát về phía Bắc 80 (km) và về phía Tây 50 (km), đồng thời cách mặt đất 4 (km). Chiếc máy bay thứ ba nằm chính giữa của chiếc máy bay thứ nhất và thứ hai, đồng thời ba chiếc máy bay này thẳng hàng.

Xác định khoảng cách của chiếc máy bay thứ ba với vị trí tại điểm xuất phát của nó. (đơn vị: km, làm tròn đến hàng phần mười).
Trả lời:
Phần mái của một căn nhà có dạng là khối đa diện được mô tả và gắn trên hệ trục tọa độ Oxyz như hình vẽ. Tính thể tích khối đa diện của mái nhà.


Trả lời:
