Bài học cùng chủ đề
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 0 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Đề kiểm tra giữa học kì I (đề số 1) SVIP

Hàm số nào sau đây nghịch biến trên khoảng (−∞;+∞)?
Cho hàm số y=f(x) có đạo hàm f′(x)=x2(x2−1). Điểm cực tiểu của hàm số y=f(x) là
Cho hàm số y=f(x) xác định, liên tục trên R và có bảng biến thiên sau:

Khẳng định nào sau đây đúng?
Số đường tiệm cận của đồ thị hàm số y=2x+32x−1 là
Đồ thị hàm số nào sau đây cắt trục tung tại điểm có tung độ âm?
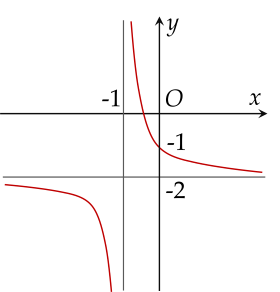
Đường cong trong hình vẽ là đồ thị của hàm số nào sau đây?
Trong không gian cho hình hộp ABCD.A′B′C′D′. Mệnh đề nào dưới đây sai?

Trong không gian Oxyz với i,j,k lần lượt là vectơ đơn vị của các trục Ox,Oy,Oz, cho a=2i+k−3j. Tọa độ của a là
Trong không gian với hệ tọa độ Oxyz,cho hai điểm A(0;−2;3), B(1;0;−1). Gọi M là trung điểm đoạn AB. Khẳng định nào sau đây là đúng?
Giá trị nhỏ nhất của hàm số y=x3+x3 trên khoảng (0;+∞) là
Đồ thị của hàm số nào sau đây có tiệm cận ngang?
Cho hàm số y=sin2x+sinx+1sinx+1. Gọi M là giá trị lớn nhất và m là giá trị nhỏ nhất của hàm số đã cho. Giá trị của M−m là
Cho hàm số y=f(x) xác định, liên tục trên R và có bảng biến thiên như sau.
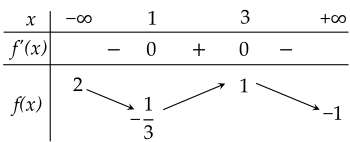
| a) Hàm số có giá trị cực đại bằng 3. |
|
| b) Hàm số có hai điểm cực trị. |
|
| c) Hàm số có giá trị lớn nhất bằng 1, nhỏ nhất bằng −31. |
|
| d) Đồ thị hàm số không cắt trục hoành. |
|
Cho hàm số y=x−1x2−2x−3.
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) Đồ thị hàm số nhận đường thẳng y=x+1 làm tiệm cận xiên. |
|
| b) Hàm số có hai điểm cực trị. |
|
| c) Gọi A,B,C là giao điểm của đồ thị hàm số với các trục Ox,Oy. Diện tích tam giác ABC bằng 6. |
|
| d) Có đúng hai giá trị nguyên của tham số m để hàm số f(x)=x−1x2−2x−3−m2x đồng biến trên từng khoảng xác định. |
|
Ông An muốn xây một cái bể chứa nước lớn dạng một khối hộp chữ nhật không nắp có thể tích bằng 288 m3. Đáy bể là hình chữ nhật có chiều dài gấp đôi chiều rộng, giá thuê nhân công để xây bể là 500000 đồng/m2. Ba kích thước của bể được mô tả như hình vẽ dưới (a (m) >0; c (m) >0).
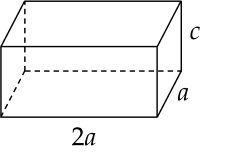
Nếu ông An biết xác định các kích thước của bể hợp lí thì chi phí thuê nhân công sẽ thấp nhất (Biết độ dày thành bể và đáy bể không đáng kể).
|
a) Diện tích các mặt cần xây là S=2a2+6ac m2. |
|
|
b) 2a2c=280. |
|
|
c) Diện tích các mặt cần xây nhỏ nhất là 216 m2. |
|
|
d) Chi phí thấp nhất để xây dựng bể đó là 108 triệu đồng. |
|
Một nhà kho gồm nền nhà OABC, bốn bức tường và hai mái nhà đều là hình chữ nhật gắn trong hệ trục tọa độ Oxyz như hình vẽ bên (đơn vị trên mỗi trục là mét).

| a) Điểm K(2;10;4) là trung điểm của EF. |
|
| b) Tọa độ của điểm A(5;0;0). |
|
| c) Trên đường thẳng vuông góc với nền nhà tại điểm K, người ta treo một bóng đèn ở vị trí H cách vị trí K một đoạn bằng 0,5 m. Khi đó khoảng cách từ bóng đèn H đến nền nhà là 4 m. |
|
| d) Điểm I(0;2;1) là vị trí bật công tắc của bóng đèn. Độ dài ngắn nhất của đường dây điện bắt từ I tới H là a (mét). Khi đó a lớn hơn 9,5 (biết đường dây điện thuộc mặt phẳng (OMQC) và (MEFQ)). |
|
Một chất điểm chuyển động theo quy luật và quãng đường di chuyển được sau t giây được tính theo công thức S(t)=−3t3+243t2 (m). Vận tốc v (m/s) của chuyển động đạt giá trị lớn nhất khi t bằng bao nhiêu giây?
Trả lời:
Người quản lí của một khu chung cư có 100 căn hộ cho thuê nhận thấy rằng tất cả các căn hộ sẽ có người thuê nếu giá thuê một căn hộ là 8 triệu đồng một tháng. Một cuộc khảo sát thị trường cho thấy rằng, trung bình cứ mỗi lần tăng giá thuê căn hộ thêm 100 nghìn đồng thì sẽ có thêm một căn hộ bị bỏ trống. Người quản lí nên đặt giá thuê mỗi căn hộ là bao nhiêu để doanh thu là lớn nhất? (đơn vị: triệu đồng)
Trả lời:
Trong không gian với hệ tọa độ Oxyz, một máy bay đang bay ở vị trí A(325;600;15) với tốc độ v=(275;369;400) gặp luồng gió có tốc độ u=(75;−36;15) (đơn vị tốc độ là km/giờ). Mất 15 phút sau, máy bay mới thoát khỏi luồng gió đó. Máy bay đã lệch đường bay theo dự tính một đoạn bao nhiêu? Giả sử đường bay là đường thẳng. (Kết quả làm tròn đến hàng phần mười)
Trả lời:
Người ta muốn làm một cái bể dạng hình hộp chữ nhật không nắp (như hình vẽ) có thể tích bằng 1 m3. Chiều cao của bể là 5dm, các kích thước khác là x m, y m với x>0 và y>0. Diện tích toàn phần của bể (không kể nắp) là hàm số S(x) trên khoảng (0;+∞).
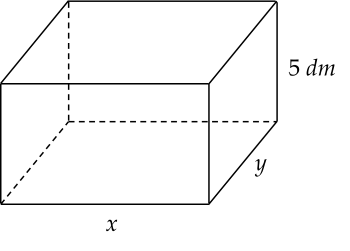
Đường tiệm cận xiên của đồ thị hàm số S(x) là đường thẳng y=ax+b. Tính P=a2+b2.
Trả lời:
Cho hàm số y=f(x) liên tục trên R. Biết rằng đồ thị của hàm số y=f′(x) được cho bởi hình vẽ sau.
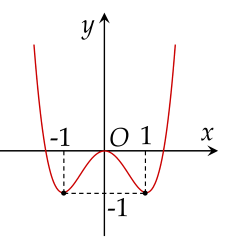
Khi đó, hàm số y=g(x)=f(x2−2) có bao nhiêu điểm cực trị?
Trả lời:
Hàm số y=(x+m)3+(x+n)3−x3 đồng biến trên khoảng (−∞;+∞). Giá trị nhỏ nhất của biểu thức P=100[4(m2+n2)−m−n] bằng bao nhiêu? (Làm tròn kết quả đến chữ số thập phân thứ nhất)
Trả lời:
