Bài học cùng chủ đề
- Đề số 1 thi thử vào 10 năm 2025 (cấu trúc 30% NLC + 40% ĐS + 30% TLN)
- Đề số 2 thi thử vào 10 năm 2025 (cấu trúc 30% NLC + 40% ĐS + 30% TLN)
- Đề số 3 thi thử vào 10 năm 2025 (cấu trúc 30% NLC + 40% ĐS + 30% TLN)
- Đề số 4 thi thử vào 10 năm 2025 (cấu trúc 30% NLC + 40% ĐS + 30% TLN)
- Đề số 5 thi thử vào 10 năm 2025 (cấu trúc 30% NLC + 40% ĐS + 30% TLN)
- Đề số 6 thi thử vào 10 năm 2025 (cấu trúc 30% NLC + 40% ĐS + 30% TLN)
- Đề số 7 thi thử vào 10 năm 2025 (cấu trúc 30% NLC + 40% ĐS + 30% TLN)
- Đề số 8 thi thử vào 10 năm 2025 (cấu trúc 30% NLC + 40% ĐS + 30% TLN)
- Đề số 9 thi thử vào 10 năm 2025 (cấu trúc 30% NLC + 40% ĐS + 30% TLN)
- Đề số 10 thi thử vào 10 năm 2025 (cấu trúc 30% NLC + 40% ĐS + 30% TLN)
- Đề số 11 thi thử vào 10 năm 2025 (cấu trúc 30% NLC + 40% ĐS + 30% TLN)
- Đề số 12 thi thử vào 10 năm 2025 (cấu trúc 30% NLC + 40% ĐS + 30% TLN)
- Đề số 13 thi thử vào 10 năm 2025 (cấu trúc 30% NLC + 40% ĐS + 30% TLN)
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Đề số 6 thi thử vào 10 năm 2025 (cấu trúc 30% NLC + 40% ĐS + 30% TLN) SVIP
Yêu cầu đăng nhập!
Bạn chưa đăng nhập. Hãy đăng nhập để làm bài thi tại đây!
Giá trị của biểu thức P=2x−3 tại x=6 là
Nghiệm của phương trình 33x−2=−2 là
Phương trình bậc hai 4x2+2mx+1=0 có hai nghiệm phân biệt, khi đó tổng hai nghiệm (S) và tích hai nghiệm (P) là
Bất phương trình 11x−3+3x+1>9x+7−1 có nghiệm là
Tất cả các giá trị của tham số m để phương trình x2+mx+4=0 có nghiệm là
Cho tam giác vuông ABC, đường cao AH.
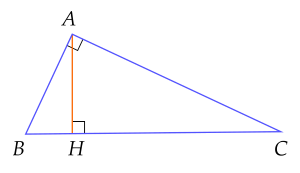
Khi đó, sinB không bằng
Hình nào dưới đây nội tiếp đường tròn?
Cho (O;5 cm) và đường thẳng a có khoảng cách đến tâm O là d. Điều kiện để a cắt hoặc tiếp xúc với (O) là
Kết quả đánh giá chất lượng bằng điểm của 40 sản phẩm được cho trong bảng sau:
Điểm | 7 | 8 | 9 | 10 |
Tần số | 7 | 14 | 16 | 3 |
Tổng số sản phẩm đạt điểm 8 và 9 là

Một chiếc thang dài 3 m. Để đảm bảo an toàn, chiếc thang phải để nghiêng một góc 65∘ so với mặt sàn. Khi đó chân thang cách chân tường một khoảng bằng
Gieo một con súc sắc cân đối, đồng chất và quan sát số chấm xuất hiện. Không gian mẫu của phép thử là
Cho ΔABC đều có cạnh 3 cm ngoại tiếp đường tròn (O,R). Giá trị của R là
Cho hệ phương trình {3(x+1)+2(x+2y)=4(1)4(x+1)−(x+2y)=9(2)
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) Điều kiện của hệ phương trình là x,y∈R. |
|
| b) Biến đổi vế trái của của phương trình (1) ta có: 7x+4y=1. |
|
| c) Biến đổi vế phải của của phương trình (2) ta có: 3x−2y=5. |
|
| d) Nghiệm của hệ phương trình là (x;y)=(1;−1). |
|
Cho phương trình x2+2(m−2)x+m2−4m=0(1) (với m là tham số)
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) Khi m=1 thì phương trình có 2 nghiệm x1=−1;x2=3. |
|
| b) Phương trình (1) có 2 nghiệm x1;x2 thoả mãn x1+x2=2(m−2);x1x2=m2−4m. |
|
| c) Giá trị của của biểu thức x12+x22=2m2−8m+16. |
|
| d) Phương trình (1) có hai nghiệm phân biệt x1;x2 thỏa mãn x13+x2=x23+x1 khi m=3. |
|
Cho tam giác ABC có góc A bằng 60∘, cạnh AB=2 cm, AC=3 cm, đường cao BE,CF cắt nhau ở H.
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) Độ dài đoạn AE bằng 1,74 cm |
|
| b) Độ dài đường cao BE bằng 3 cm. |
|
| c) Diện tích của tam giác ABC bằng 5,20 cm2. |
|
| d) Tỉ số độ dài BCFE bằng 2 cm. |
|
Minh có 2 chiếc kẹo màu: xanh (X), vàng (V). An có 2 chiếc kẹo màu: đỏ (Đ) và trắng (T). Hằng muốn ngẫu nhiên 2 chiếc kẹo từ hai bạn Minh và An (lấy mỗi bạn 1 chiếc kẹo) cùng lúc. Kết quả thu được cho ở bảng dưới đây:
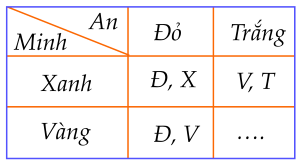
| a) Số kết quả có thể xảy ra của phép thử "Lấy ngẫu nhiên 2 chiếc kẹo từ hai bạn Minh và An cùng lúc" là 4. |
|
| b) Hằng có thể lấy 1 chiếc kẹo màu xanh và 1 chiếc kẹo vàng cùng lúc. |
|
| c) Kết quả cần điền vào ô còn trống trên bảng là (T,V). |
|
| d) Bảng trên có một ô bị sai là (Đ,X). |
|

Cổng trường Đại học Bách Khoa Hà Nội có dạng đường cong parabol, người ta đo được khoảng cách giữa 2 chân cổng là L=9 m. Nếu đứng cách chân cổng 0,5 m thì đầu chạm cổng, biết người này cao 1,6 m. Chiều cao của cổng bằng bao nhiêu m? (làm tròn đến hàng phần mười)
Trả lời:
Nghiệm của phương trình 5−x.(2x−3)=2.(1−x2) bằng bao nhiêu?
Trả lời:
Cho các số thực a,b,c thỏa mãn 0≤a,b,c≤2 và a+b+c=3. Giá trị lớn nhất của P=a3+b3+c3 bằng bao nhiêu?
Trả lời:
Cho tam giác ABC vuông tại A. Điểm E di động trên cạnh AB, qua B vẽ một đường thẳng vuông góc với CE tại D và cắt tia CA tại H. Biết BCA=30∘, số đo HDA bằng bao nhiêu độ?
Trả lời:
Một cốc thủy tinh đựng đầy nước có chiều cao 10 cm và thể tích 90π cm3. Người ta thả vào cốc một viên bi sắt hình cầu có bán kính bằng bán kính đáy cốc nước, viên bi sắt ngập toàn bộ trong nước. Lượng nước bị tràn ra ngoài bằng bao nhiêu cm3 ? (làm tròn kết quả đến hàng đơn vị)

Trả lời:
Hàng ngày Minh đều đi xe Buýt tới trường. Minh ghi lại thời gian chờ xe của mình trong 20 lần liên tiếp ở bảng sau:
Thời gian chờ | Số lần |
1 phút | 4 |
2 phút | 10 |
5 phút | 4 |
10 phút | 2 |
Tần số tương đối của thời gian mà Minh chờ xe Buýt dưới 5 phút bằng bao nhiêu? (kết quả ghi dưới dạng số thập phân)
Trả lời:
