Đề 5 thi thử vào 10 năm 2025 - Cấu trúc 100% trắc nghiệm

Câu 1 (1đ):

Hai bạn $A$ và $B$ cùng làm chung một công việc thì hoàn thành sau $8$ ngày. Nếu làm một mình xong công việc thì $B$ làm lâu hơn $A$ là $12$ ngày. Gọi thời gian $A$ , $B$ làm một mình xong công việc lần lượt là $x$ (ngày) và $y$ (ngày) $(y>x>0;y>12 )$ . Biểu thức thể hiện lượng công việc hai bạn cùng hoàn thành được trong một ngày là

\dfrac{1}{x}+\dfrac{1}{y}=8

.

x+y=8

.

x+y=\dfrac{1}{8}

.

\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{8}

.

Câu 2 (1đ):

Cho các hàm số $y=x^2;\,y=\dfrac{4x^2}{9};\,y=\dfrac{2}{x^2};\,y=\sqrt{3}x^2$ . Có bao nhiêu hàm số có dạng $y=ax^2\,(a\ne 0 )$ ?

2

.

3

.

4

.

1

.

Câu 3 (1đ):

Cho phương trình $ax^2+bx+c=0\,\,(a\ne 0 )$ có biệt thức $\Delta =b^2-4ac$ . Phương trình đã cho có nghiệm khi:

\Delta \lt 0

.

\Delta >0

.

\Delta \ge 0

.

\Delta =0

.

Câu 4 (1đ):

Cho biết $a\lt b$ , bất đẳng thức đúng là

5a-2>5b-2

.

5a+7\lt 5b+7

.

-3a\lt -3b

.

2a>2b

.

Câu 5 (1đ):

Giá trị nhỏ nhất của biểu thức $T=x+\dfrac{2}{2x-1}$ với $x>\dfrac{1}{2}$ là phân số tối giản $\dfrac{a}{b}$ . Giá trị $a+b$ bằng

5

.

7

.

3

.

9

.

Câu 6 (1đ):

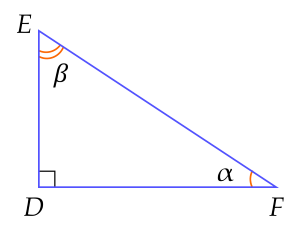
Trong hình vẽ, biết $\widehat{DFE}=\alpha,\,\widehat{DEF}=\beta$ . Khẳng định không đúng là

loading...

\cot \alpha =\dfrac{1}{\tan \alpha }

.

0\lt \cos \alpha \lt 1

.

\sin \alpha =\cos \beta

.

\tan \alpha =\dfrac{\cos \alpha }{\sin \alpha }

.

Câu 7 (1đ):

Hình cầu tâm $O$ bán kính $R$ được tạo ra khi quay

nửa đường tròn tâm

O

bán kính

R

quanh đường kính của nó.

tam giác vuông quanh cạnh góc vuông.

nửa hình tròn tâm

O

bán kính

R

quanh đường kính của nó.

hình chữ nhật quanh một cạnh của nó.

Câu 8 (1đ):

Độ dài cung tròn $60^\circ$ của một đường tròn có đường kính bằng $5$ cm là (lấy $\pi \,\approx 3,14$ , kết quả làm tròn đến chữ số thập phân thứ $2$ )

l\approx 2,6

cm.

l\approx 2,61

cm.

l\approx 2,616

cm.

l\approx 2,62

cm.

Câu 9 (1đ):

Một chiếc nón lá có đường sinh bằng $30$ cm, đường kính đáy bằng $40$ cm. Người ta dùng hai lớp lá để phủ lên bề mặt xung quanh của nón. Diện tích lá cần dùng cho một chiếc nón đó là

1\,200\pi

cm².

900\pi

cm².

1\,000\pi

cm².

1\,100\pi

cm².

Câu 10 (1đ):

Xét phép thử "Viết ngẫu nhiên một số tự nhiên có hai chữ số lớn hơn $70$ ". Số phần tử của không gian mẫu là

29

.

30

.

70

.

10

.

Câu 11 (1đ):

Một hộp có $10$ quả bóng với kích thước và khối lượng như nhau, được đánh số từ $11$ đến $19$ . Chọn ngẫu nhiên một quả bóng trong hộp, số phần tử của không gian mẫu là

10

.

11

.

2

.

20

.

Câu 12 (1đ):

Một bó hoa gồm $1$ bông hoa màu đỏ, $1$ bông hoa màu hồng và $1$ bông hoa màu vàng. Bạn Linh chọn ngẫu nhiên $2$ bông hoa từ bó hoa đó. Số kết quả thuận lợi cho biến cố “Trong $2$ bông hoa được chọn ra, có duy nhất $1$ bông hoa màu đỏ” là

1

.

2

.

4

.

3

.

Câu 13 (1đ):

Khẳng định sau đúng hay sai?

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Bất phương trình $\dfrac{8-3x}{2}-x\lt 5$ vô nghiệm.
b) Bất phương trình $(x+3 )(x+4 )>(x-2 )(x+9 )+25$ có vô số nghiệm $x\in\mathbb{R}$ .
c) Bất phương trình $0,7x+\dfrac{2x-4}{3}-\dfrac{x}{6}>1$ có nghiệm $x>\dfrac{35}{18}$ .
d) Bất phương trình $(x-1 )^2\lt x(x+3)$ có nghiệm $x\lt 0,2$ .

Câu 14 (1đ):

Cho phương trình $\sqrt{9(x-1)^2}=6$ .

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Điều kiện xác định của phương trình là $x\ge1$ .
b) Phương trình trên tương đương với phương trình $3\|x-1\|=6$ .
c) Phương trình có một nghiệm là $x=1$ .
d) Phương trình có hai nghiệm phân biêt.

Câu 15 (1đ):

Cho tam giác $ABC$ có đường cao $AH$ , $H$ nằm giữa $B$ và $C$ . Biết $HB=3$ cm; $HC=6$ cm; $\widehat{HAC}=60^\circ$ . (Độ dài đoạn thẳng làm tròn đến chữa số thập phân thứ nhất, số đo góc làm tròn đến độ)

(Nhấp vào ô màu vàng để chọn đúng / sai)

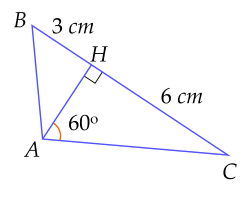
a) Số đo góc $ACH$ bằng $40^\circ$ .
b) Cạnh $AC=\dfrac{3}{\sqrt{3}}$ cm.
c) Số đo góc $BAC$ bằng $101^\circ$ .
d) Độ dài cạnh $AB$ bằng $3$ cm.

Câu 16 (1đ):

Cuối học kì $I$ , thầy giáo chủ nhiệm liệt kê số ngày nghỉ học của học sinh lớp 7A bằng bảng sau:

$1$	$0$	$3$	$0$	$5$
$3$	$2$	$5$	$1$	$3$
$0$	$1$	$1$	$4$	$1$
$2$	$3$	$4$	$0$	$5$
$0$	$2$	$0$	$0$	$2$
$0$	$1$	$3$	$2$	$4$
$2$	$1$	$2$	$2$	$3$
$0$	$2$	$1$	$0$	$1$

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Bảng trên có $5$ giá trị khác nhau.
b) Lớp 7A có $40$ học sinh.
c) Biểu đồ cột về tần số ngày nghỉ của học sinh lớp 7A có dạng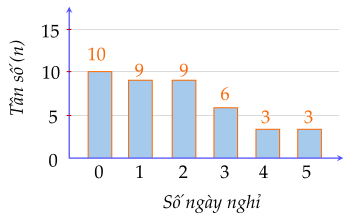
d) Tần số tương đối của số học sinh không nghỉ ngày nào là $10\%$ .

Câu 17 (1đ):

Cho hàm số $y=(2m-1 )x^2$ ( $m$ là tham số, $m\ne 0,5$ ), biết rằng đồ thị của hàm số này đi qua điểm có hoành độ bằng $1$ và tung độ bằng $2$ , vậy giá trị của $m$ bằng bao nhiêu?

Trả lời:

Câu 18 (1đ):

Có bao nhiêu giá trị nguyên của $m$ để phương trình $mx^2+4(m+1)x-2m=0$ có nghiệm duy nhất?

Trả lời:

Câu 19 (1đ):

Cho biểu thức $A=-x^2+2x-1$ . Giá trị lớn nhất của $A$ đạt được khi $x$ bằng bao nhiêu?

Trả lời:

Câu 20 (1đ):

Cho $\Delta ABC$ cân tại $A$ có $\widehat{BAC}=120^\circ$ . Trên nửa mặt phẳng bờ $BC$ không chứa đỉnh $A$ , lấy $D$ sao cho $BCD$ là tam giác đều. Khi đó tứ giác $ABCD$ có tổng hay góc $A$ và $D$ bằng bao nhiêu độ ?

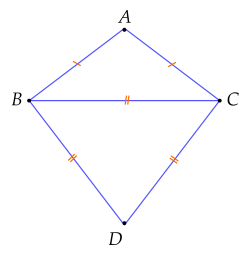
loading...

Trả lời:

Câu 21 (1đ):

Một khúc sông rộng khoảng $280$ m. Một chiếc đò chèo qua sông bị dòng nước đẩy xiên nên phải chèo khoảng $340$ m mới sang được bờ bên kia. Dòng nước đã đẩy con thuyền đó đi một góc bao nhiêu (làm tròn đến hàng đơn vị của độ)?

Trả lời:

Câu 22 (1đ):

Người ta thiết kế một công trình kiến trúc như hình dưới đây.

Mái nhà là $3$ hình nón có kích thước giống nhau, chiều cao bằng $\dfrac{1}{2}$ chiều rộng của hình nón. Chiều cao của mái nhà là giá trị nhỏ nhất của biểu thức:

$h=\dfrac{1}{a^2+4b^2}+\dfrac{1}{b^2+ 4a^2}+\dfrac{4}{10ab}$ thỏa mãn $a,\,b >0$ ; $a+ b= 1$ . (đơn vị là $m$ )

Số tiền sơn mặt trên của mái nhà bằng bao nhiêu, biết giá $1$ (m²) $= 200\,000$ đồng?

( $\pi=3,14$ kết quả làm tròn đến hàng đơn vị).

Trả lời:

Bài học cùng chủ đề

Đề số 4 thi thử vào 10 năm 2025 (cấu trúc 30% NLC + 40% ĐS + 30% TLN) SVIP

Yêu cầu đăng nhập!

$1$	$0$	$3$	$0$	$5$
$3$	$2$	$5$	$1$	$3$
$0$	$1$	$1$	$4$	$1$
$2$	$3$	$4$	$0$	$5$
$0$	$2$	$0$	$0$	$2$
$0$	$1$	$3$	$2$	$4$
$2$	$1$	$2$	$2$	$3$
$0$	$2$	$1$	$0$	$1$

$1$	$0$	$3$	$0$	$5$
$3$	$2$	$5$	$1$	$3$
$0$	$1$	$1$	$4$	$1$
$2$	$3$	$4$	$0$	$5$
$0$	$2$	$0$	$0$	$2$
$0$	$1$	$3$	$2$	$4$
$2$	$1$	$2$	$2$	$3$
$0$	$2$	$1$	$0$	$1$

Bài học cùng chủ đề

Báo cáo học liệu

Mua học liệu

Mua học liệu:

Số dư ví của bạn: 0 coin - 0 Xu

Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu

Để nhận Coin\Xu, bạn có thể:

Chi tiết xem tại đây

Thông tin của bạn

Đề số 4 thi thử vào 10 năm 2025 (cấu trúc 30% NLC + 40% ĐS + 30% TLN) SVIP

Yêu cầu đăng nhập!

Truy vết IP log

Báo lỗi câu hỏi

Các khóa học có thể bạn quan tâm

Yêu cầu VIP

$1$	$0$	$3$	$0$	$5$
$3$	$2$	$5$	$1$	$3$
$0$	$1$	$1$	$4$	$1$
$2$	$3$	$4$	$0$	$5$
$0$	$2$	$0$	$0$	$2$
$0$	$1$	$3$	$2$	$4$
$2$	$1$	$2$	$2$	$3$
$0$	$2$	$1$	$0$	$1$