Bài học cùng chủ đề
- Đề số 1 thi thử vào 10 năm 2025 (cấu trúc 30% NLC + 40% ĐS + 30% TLN)
- Đề số 2 thi thử vào 10 năm 2025 (cấu trúc 30% NLC + 40% ĐS + 30% TLN)
- Đề số 3 thi thử vào 10 năm 2025 (cấu trúc 30% NLC + 40% ĐS + 30% TLN)
- Đề số 4 thi thử vào 10 năm 2025 (cấu trúc 30% NLC + 40% ĐS + 30% TLN)
- Đề số 5 thi thử vào 10 năm 2025 (cấu trúc 30% NLC + 40% ĐS + 30% TLN)
- Đề số 6 thi thử vào 10 năm 2025 (cấu trúc 30% NLC + 40% ĐS + 30% TLN)
- Đề số 7 thi thử vào 10 năm 2025 (cấu trúc 30% NLC + 40% ĐS + 30% TLN)
- Đề số 8 thi thử vào 10 năm 2025 (cấu trúc 30% NLC + 40% ĐS + 30% TLN)
- Đề số 9 thi thử vào 10 năm 2025 (cấu trúc 30% NLC + 40% ĐS + 30% TLN)
- Đề số 10 thi thử vào 10 năm 2025 (cấu trúc 30% NLC + 40% ĐS + 30% TLN)
- Đề số 11 thi thử vào 10 năm 2025 (cấu trúc 30% NLC + 40% ĐS + 30% TLN)
- Đề số 12 thi thử vào 10 năm 2025 (cấu trúc 30% NLC + 40% ĐS + 30% TLN)
- Đề số 13 thi thử vào 10 năm 2025 (cấu trúc 30% NLC + 40% ĐS + 30% TLN)
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Đề số 7 thi thử vào 10 năm 2025 (cấu trúc 30% NLC + 40% ĐS + 30% TLN) SVIP
Yêu cầu đăng nhập!
Bạn chưa đăng nhập. Hãy đăng nhập để làm bài thi tại đây!
Phương trình bậc nhất hai ẩn ax+by=c (với a, b là các số thực, thỏa mãn a=0 hoặc b=0) luôn
Hai xe máy cùng đi quãng đường từ Hà Nội về Hải Phòng. Xe thứ nhất đi hết 3 giờ 20 phút, xe thứ hai đi hết 3 giờ 40 phút. Biết vận tốc xe máy thứ nhất nhanh hơn vận tốc xe máy thứ hai là 3 km. Gọi vận tốc xe thứ nhất là x (km/h), (x>3), vận tốc xe thứ hai là y (km/h). Biểu thức thể hiện mối quan hệ giữa x và y là
Theo kế hoạch, một tổ công nhân phải sản xuất 360 chai nước rửa tay khô. Đến khi làm việc, do phải điều 3 công nhân đi làm việc khác nên mỗi công nhân còn lại phải sản xuất nhiều hơn dự định là 4 chai. Giả sử năng suất lao động của mỗi công nhân là như nhau, gọi số công nhân ban đầu của tổ là x (người) (x∈N∗,x>3) thì biểu thức biểu diễn số chai nước rửa tay khô thực tế mỗi công nhân đã sản xuất là
Công thức tính diện tích hình quạt tròn n∘ là
Hình nón có đường sinh l, đường cao h, bán kính đáy r. Khẳng định đúng là
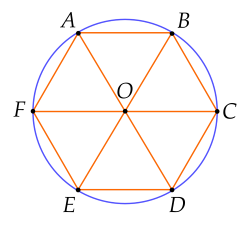
Số đo của góc MON trong hình vẽ dưới đây là

Cho lục giác đều ABCDEF nội tiếp đường tròn (O). Phép quay thuận chiều a∘ tâm O biến điểm A thành điểm C, giá trị của a là
Đồ thị hàm số y=ax2 (a=0) đi qua điểm B(−2;1). Khi đó giá trị của a là
Tập hợp Ω={1;2;3;4;5;6} mô tả không gian mẫu của phép thử nào dưới đây?
Một hộp có hai viên bi trắng được đánh số từ 1 đến 2, ba viên bi xanh được đánh số từ 3 đến 5 và hai viên bi đỏ được đánh số từ 6 đến 7. Lấy ngẫu nhiên hai viên bi, tập hợp M={(1,2);(3,4);(3,5);(4,5);(6,7)} biểu diễn các kết quả thuận lợi của biến cố nào dưới đây?
Cho a là số không âm, b là số dương. Khẳng định đúng là
Điều kiện xác định của căn thức 2x−3 là
Phương trình 2x+5y=7 (3) có công thức nghiệm tổng quát là {x∈Ry=ax+b.
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) Cặp số (1;−1) là nghiệm của phương trình (3). |
|
| b) Áp dụng quy tắc chuyển vế ta thu được phương trình 5y=−2x+7. |
|
| c) Giá trị của hệ số a trong công thức nghiệm bằng −0,4. |
|
| d) Giá trị của hệ số b trong công thức nghiệm bằng 7. |
|
Bác Thời vay 2000000 đồng của ngân hàng làm kinh tế gia đình trong thời hạn 1 năm. Lẽ ra cuối năm bác phải trả cả vốn lẫn lãi, song bác đã được ngân hàng cho kéo dài thời hạn thêm năm nữa. Số lãi của năm đầu được gộp vào vốn để tính lãi năm sau và lãi suất như cũ. Hết 2 năm bác phải trả tất cả 2420000 đồng. Gọi lãi suất cho vay một năm là x% (x>0).
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) Nếu lãi suất là 8% thì sau 1 năm bác Thời phải trả tiền lãi là 160000 đồng. |
|
| b) Sau 1 năm cả vốn lẫn lãi sẽ là 2000000+2000000x (đồng). |
|
| c) x đã cho là nghiệm của phương trình x2+200x−2100=0. |
|
| d) Lãi suất cho vay là 10% một năm. |
|
Cho ΔABC đều ngoại tiếp (O), biết (O) có bán kính 3 cm, AH là đường cao.
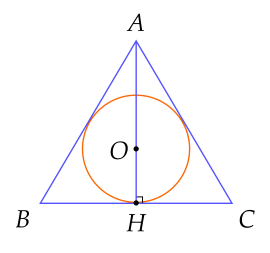
| a) OA=3 cm. |
|
| b) AH=9 cm. |
|
| c) BC=36 cm. |
|
| d) Diện tích ΔABC bằng 273 cm2. |
|
Tổ 1 của lớp 6A gồm 5 bạn học sinh gồm 3 nam (là bạn A, B, C) và 2 bạn nữ (là bạn D, E). Chọn ngẫu nhiên 2 bạn từ tổ 1 (gồm 1 nam và 1 nữ) cùng lúc.
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) Công việc trên là một phép thử ngẫu nhiên. |
|
| b) Một trong các kết quả có thể xảy ra là (D,E). |
|
| c) Có tất cả 6 kết quả có thể xảy ra. |
|
| d) Nếu chọn ngẫu nhiên một bạn từ tổ 1 thì xác suất để bạn được chọn là nữ bằng 53. |
|
Hà có 4 hộp kẹo dẻo với 4 vị khác nhau là: vị dâu, vị cam, vị nho, vị việt quất. Hà lấy ngẫu nhiên một hộp kẹo trong 4 hộp kẹo này cho Hải. Hải ghi lại vị của hộp kẹo nhận được rồi trả hộp kẹo lại cho Hà. Tiếp theo Hà lại lấy ngẫu nhiên một hộp kẹo trong 4 hộp kẹo đó đưa cho Hải để ghi lại vị của hộp kẹo nhận được trong lần thứ hai. Quan sát vị của hộp kẹo qua hai lần lấy. Không gian mẫu của phép thử này có bao nhiêu số phần tử?
Trả lời:
Người ta cắt 31 tấm tôn hình tròn rồi cuộn lại thành hình nón.
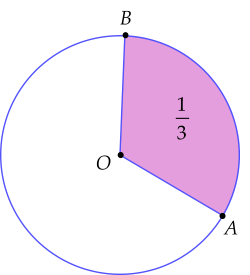
Biết chiều dài AB là giá trị nhỏ nhất của biểu thức AB=m−1n2+n−1m2, với n>1; m>1 (đơn vị của AB là cm). Diện tích xung quanh của hình nón bằng bao nhiêu cm2? (làm tròn kết quả đến hàng đơn vị).
Trả lời:
Rút gọn biểu thức A=6−15+23−236 ta được kết quả bằng bao nhiêu?
Trả lời:
Cho biểu thức A=4y2−4y+3 với −5≤y≤−1. Giá trị lớn nhất của biểu thức A bằng bao nhiêu?
Trả lời:
Cho hàm số y=ax2. Gọi A và B là hai điểm thuộc đồ thị hàm số sao cho A,B là có cùng tung độ dương, hoành độ của A bằng 1 và tam giác OAB là tam giác vuông có diện tích bằng 2. Giá trị của a bằng bao nhiêu?
Trả lời:
Cho đường tròn tâm O đường kính BC, điểm A thuộc đường tròn. Vẽ đường thẳng qua O song song với BA cắt tiếp tuyến của đường tròn (O) tại C ở I, OI cắt AC tại H.
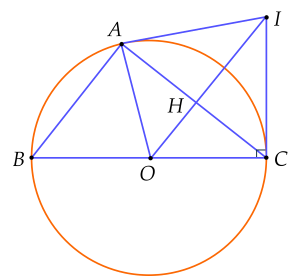
Biết BC=30 cm, AB=18 cm, độ dài AI bằng bao nhiêu cm? (kết quả làm tròn đến hàng đơn vị).
Trả lời:
