Đáp án đề tuyển sinh vào lớp 10 tỉnh Hải Dương năm 2021 - 2022 SVIP

Hướng dẫn giải:

a) Ta có: $x^{2}-3 x=4 \Leftrightarrow x^{2}-3 x-4=0$

$\Leftrightarrow\left[\begin{aligned} &x=-1 \\ &x=4 \\ \end{aligned}\right.$.

Vậy phương trình có hai nghiệm: $x=-1$ và $x=4$.

b) Hệ phương trình $\left\{\begin{aligned}&2 x-5-y=0 \\ &5 x+3 y=18\end{aligned}\right. \Leftrightarrow\left\{\begin{aligned}&2 x-5=y \, \text { (1) } \\ &5 x+3 y=18 \, \text { (2) }\end{aligned}\right.$

Thế $y$ ở $(\text{1})$ vào $(\text{2})$ ta được: $5 x+3(2 x-5)=18 \Leftrightarrow 11 x=33 \Leftrightarrow x=3$.

Thay ${x}=3$ vào $(\text{1})$ ta được ${y}=1.$

Vậy hệ có nghiệm $(x;y) =(3 ; 1)$.

Hướng dẫn giải:

a) Ta có: $P=\dfrac{2 \sqrt{a}}{\sqrt{a}+3}+\dfrac{\sqrt{a}+1}{\sqrt{a}-3}+\dfrac{-7 \sqrt{a}-3}{(\sqrt{a}-3)(\sqrt{a}+3)}$

$=\dfrac{2 \sqrt{{a}}(\sqrt{{a}}-3)+(\sqrt{{a}}+1)(\sqrt{{a}}+3)-7 \sqrt{{a}}-3}{(\sqrt{{a}}-3)(\sqrt{{a}}+3)}$

$=\dfrac{2 a-6 \sqrt{a}+a+4 \sqrt{a}+3-7 \sqrt{a}-3}{(\sqrt{a}-3)(\sqrt{a}+3)}$

$=\dfrac{3 a-9 \sqrt{a}}{(\sqrt{a}-3)(\sqrt{a}+3)}=\dfrac{3 \sqrt{a}(\sqrt{a}-3)}{(\sqrt{a}-3)(\sqrt{a}+3)}=\dfrac{3 \sqrt{a}}{\sqrt{a}+3}$

Vậy ${P}=\dfrac{3 \sqrt{{a}}}{\sqrt{{a}}+3}$ với ${a} \geq 0, {a} \neq 9$.

b) Hàm số $y=ax-4$ là hàm số bậc nhất và cắt đường thẳng $(d)$ khi:

   $a \neq 0$ và $a \neq-3$.

Thay ${y}=5$ vào phương trình đường thẳng $({d})$ ta được:

   $5=-3 x+2 \Leftrightarrow x=-1$.

Thay $x=-1$, $y=5$ vào phương trình $y={a} x-4$ ta được:

   $5=-a-4 \Leftrightarrow a=-9$ (thỏa mãn).

Vậy $a=-9$ là giá trị cần tìm.

Hướng dẫn giải:

a) Gọi chiều dài của mảnh đất hình chữ nhật ban đầu là ${x}$ (m), chiều rộng của mảnh đất hình chữ nhật ban đầu là ${y}$ (m).

Điều kiện: $0<x<12$, $1<{y}<12$.

Ta có phương trình $2(x+y)=24$ (1).

Diện tích mảnh đất hình chữ nhật ban đầu là: $x . y$ (m$^2$).

Chiều dài khi tăng lên $2$ m là: ${x}+2$ (m), chiều rộng khi giảm đi $1$ m là: ${y}-1$ (m).

Diện tích mảnh đất hình chữ nhật khi thay đổi là: $({x}+2)({y}-1)$ (m$^2$).

Ta có phương trình: $(x+2)(y-1)-x y=1 \Leftrightarrow-x+2 y=3$ (2)

Từ (1) và (2) ta có hệ phương trình: $\left\{\begin{aligned}&2(x+y)=24 \\ &-x+2 y=3\end{aligned} \Leftrightarrow\left\{\begin{aligned}&x=7 \\ &y=5\end{aligned}\right.\right.$ (thỏa mãn).

Vậy mảnh đất hình chữ nhật ban đầu có chiều dài là $7$ (m), chiều rộng là $5$ (m).

b) Ta có: $\Delta'=[-(m-1)]^{2}-1 .(m-3)=m^{2}-3 m+4=\left(m-\dfrac{3}{2}\right)^{2}+\dfrac{7}{4}>0$ với mọi ${m}$ nên phương trình đã cho luôn có hai nghiệm phân biệt $x_{1}$ và $x_{2}$ với mọi $m$.

Theo hệ thức Vi-ét ta có: $x_{1}+x_{2}=2(m-1)$; $x_{1} \cdot x_{2}=m-3$.

Ta có: $\left|x_{1}-x_{2}\right|=4 \Leftrightarrow\left(x_{1}-x_{2}\right)^{2}=16 \Leftrightarrow\left(x_{1}+x_{2}\right)^{2}-4 x_{1} x_{2}=16$.

Từ đó ta được phương trình: $4(m-1)^{2}-4(m-3)=16$

$ \Leftrightarrow 4 m^{2}-12 m=0 \Leftrightarrow\left[\begin{aligned}&m=0 \\ &m=3\end{aligned}(\text{tm})\right.$.

Vậy ${m}=0$, $m=3$ là các giá trị cần tìm.

Hướng dẫn giải:

1a)

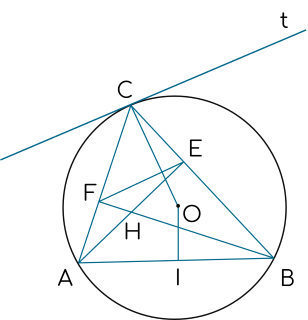
Gọi $I$ là trung điểm của ${AB}$, do $A E \perp B C \Rightarrow \widehat{A E B}=90^{\circ} \Rightarrow I A=I E=I B$ (1).

Do $B F \perp A C \Rightarrow \widehat{B F A}=90^{\circ} \Rightarrow I A=I B=I F$ (2).

Từ (1) và (2) suy ra: ${IA}={IB}={IE}={IF}$.

Do đó bốn điểm ${A}, \, {B}, \, {E}, \, F$ cùng nằm trên đường tròn đường kính ${AB}$.

1b) Kẻ tiếp tuyến ${Ct}$ của đường tròn $({O} ; {R})$.

Ta có: $\widehat{B C t}=\widehat{B A C}$ (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung ${BC}$).

Mà $\widehat{B A C}=\widehat{C E F}$ (góc ngoài và góc trong tại đỉnh đối diện của tứ giác nội tiếp $ABEF$).

Dó đó: $\widehat{B Ct} =\widehat{C E F}$, mà hai góc này ở vị trí so le trong nên $C t / / E F$.

Do $O C \perp C t$ suy ra $O C \perp E F$ (đpcm).

2.

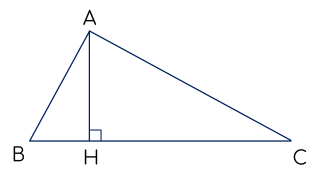
Do $\widehat{B}$ và $\widehat{C}$ là góc nhọn nên hình chiếu $H$ của ${A}$ trên ${BC}$ nằm giữa ${B}$ và ${C}$.

Áp dụng định lí Py-ta-go ta có: $A B^{2}=A H^{2}+H B^{2}$; $A C^{2}=A H^{2}+H C^{2}$.

Suy ra $2 B C^{2}+A C^{2}+A B^{2}=2 B C^{2}+2 A H^{2}+H B^{2}+H C^{2}$.

$(H B-H C)^{2} \geq 0 \Rightarrow H C^{2}+H B^{2} \geq 2 H C.{HB} \Rightarrow 2\left(H C^{2}+H B^{2}\right) \geq(H C+{HB})^{2}=B C^{2}$.

Do đó $2 B C^{2}+A C^{2}+A B^{2} \geq \dfrac{5}{2} B C^{2}+2 A H^{2} \geq 2 \sqrt{5}.B C.A H=4 \sqrt{5} .S_{A B C}$

Dấu "=" xảy ra khi ${HB}={HC}$ và $B C=\dfrac{2 \sqrt{5}}{5}.A H$.

Vậy giá trị nhỏ nhất của ${P}=2 B C^{2}+A C^{2}+A B^{2}$ là $4 \sqrt{5}.S_{A B C}$, khi tam giác ${ABC}$ cân tại ${A}$ có chiều cao $A H=\dfrac{\sqrt{5}}{2} B C$.

Hướng dẫn giải:

Đặt $a=\sqrt{y}>0,$ $b=\sqrt{2 x+3}>0 \Rightarrow y=a^{2},$ $2 x+3=b^{2}$, thay vào giả thiết ta được:

   $a\left(a^{2}+1\right)-3 b^{2}=\left(b^{2}+1\right) b-3 a^{2} \Leftrightarrow a^{3}-b^{3}+3\left(a^{2}-b^{2}\right)+(a-b)=0$

$\Leftrightarrow(a-b)\left(a^{2}+a b+b^{2}+3 a+3 b+1\right)=0$.

Suy ra: ${a}={b}$ vì $a^{2}+a b+b^{2}+3 a+3 b+1>0 \Rightarrow \sqrt{y}=\sqrt{2 x+3} \Leftrightarrow y=2 x+3$.

Thay ${y}=2 {x}+3$ vào ${M}$ ta được: $M=x(2 x+3)+3(2 x+3)-3-4 x^{2}=-2 x^{2}+9 x+6$

$M=-2\left(x-\dfrac{9}{4}\right)^{2}+\dfrac{129}{8} \leq \dfrac{129}{8}$.

Vậy ${M}_{\max }=\dfrac{129}{8}$ khi $x=\dfrac{9}{4},$ $y=\dfrac{15}{2}$.