Trong không gian $Oxyz$, cho $A\left(0\,;\,-1\,;\,-1 \right)$, $B\left(-2\,;\,1\,;\,1 \right)$, $C\left(-1\,;\,3\,;\,0 \right)$,$D\left(1\,;\,1\,;\,1 \right)$. Côsin của góc giữa hai đường thẳng $AB$ và $CD$ bằng

Trong không gian với hệ tọa độ $Oxyz$, cho hai đường thẳng $d_1:\left\{ \begin{aligned}& x=\,t \\& y=1-2t \\& z=-3t \end{aligned} \right.\,\,\left(t\in \mathbb{R} \right)$ và đường thẳng $d_2:\dfrac{x}{-4}=\dfrac{y-1}{1}=\dfrac{z+1}{5}$. Góc giữa hai đường thẳng $d_1,\,d_2$ là

Trong không gian với hệ tọa độ $Oxyz$, cho hai đường thẳng $d_1$ và đường thẳng $d_2$ lần lượt có véc-tơ chỉ phương là $\overrightarrow{u_{d_1}}=(1;\,-2;\,-3)$ và $\overrightarrow{u_{d_2}}=(-4;\,1;\,5)$. Góc giữa hai đường thẳng $d_1,\,d_2$ là

Trong không gian $Oxyz,$ cho đường thẳng $d$ có VTCP $\overrightarrow{u}=(2;2;1 ).$Gọi $\alpha$ là góc giữa $d$ và trục $Ox$. Tính $\cos \alpha.$

Trong không gian $Oxyz$, cho hai điểm $A( 1;0;0 );\,B( 0;\sqrt{2};0 )$ và các đường thẳng $d_1:\dfrac{x+1}{1}=\dfrac{y}{-\sqrt{2}}=\dfrac{z-2}{1}$ ,$d_2:\dfrac{x+1}{1}=\dfrac{y-2}{-2}=\dfrac{z+3}{1}$, $\Delta :\left\{ \begin{aligned} & x=2+t \\ & y=1+\sqrt{2}t \\ & z=2+mt \end{aligned} \right.$.

Trong không gian với hệ tọa độ $Oxyz$. Góc tạo bởi đường thẳng $d:\dfrac{x+3}{2}=\dfrac{y-2}{1}=\dfrac{z+1}{1}$ và mặt phẳng $(P):3x+4y+5z+3=0$ bằng bao nhiêu độ?

Cho $M (-3; -1; 3)$ và $N (-1; 0; 2)$ và mặt phẳng $(P): x + 2y + z + 4 = 0$. Góc giữa đường thẳng $MN$ và mặt phẳng $(P)$ bằng bao nhiêu độ?

Trong không gian với hệ tọa độ $Oxyz,$ góc giữa trục $Oz$ và mặt phẳng $(P):x-y+\sqrt{2}z+2\,024=0$ bằng

Trong không gian với hệ tọa độ $Oxyz,$ cho hai đường thẳng $d_1:\dfrac{x-1}{2}=\dfrac{y-2}{-2}=\dfrac{z+1}{-1},$ $d_2:\left\{ \begin{aligned}& x=t \\& y=0 \\& z=-t \end{aligned} \right..$ Phương trình mặt phẳng $(P )$ chứa đường thẳng $d_1$ tạo với đường thẳng $d_2$ một góc $45^\circ$ là

Trong không gian $Oxyz$, $\cos$ của góc giữa mặt phẳng $(Oxy)$ và mặt phẳng $(P):x+y+z-2=0$ bằng

Trong không gian với hệ tọa độ $Oxyz$, cho hình chóp $S.ABCD$ có các đỉnh lần lượt là

$S(0;0;a)$; $A(0; 0; 0)$; $B(2a; 0; 0)$; $D\Big(0; \dfrac{2a\sqrt{3}}{3}; 0 \Big)$ với $a>0$.

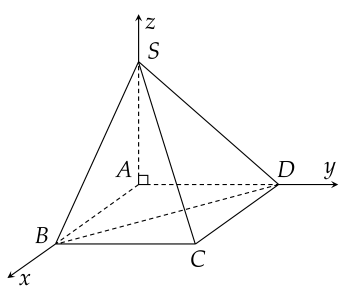
Góc giữa hai mặt phẳng $(SBD)$ và $(ABCD)$ bằng