Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Dạng 3. Tương giao của hai đồ thị hàm số SVIP
Tải đề xuống bằng file Word
Yêu cầu đăng nhập!
Bạn chưa đăng nhập. Hãy đăng nhập để làm bài thi tại đây!
Đồ thị hàm số nào sau đây cắt trục tung tại điểm có tung độ âm?
Đồ thị hàm số y=x3−6x2+11x−6 cắt trục hoành tại bao nhiêu điểm phân biệt?
Giao điểm của đồ thị hàm số y=−x3+5x−2 với trục tung có toạ độ là
Số giao điểm của đồ thị hàm số y=−2x4+x2+23 và trục hoành là
Đồ thị hàm số y=2x−12x+1 có tọa độ giao điểm với trục tung là
Đồ thị của hàm số nào sau đây không cắt trục hoành?
Đồ thị hàm số y=x−23x+6 cắt trục hoành tại điểm có hoành độ bằng
Đồ thị hàm số y=3x2+x+2 và trục tung có bao nhiêu điểm chung?
Số giao điểm của đồ thị hàm số y=x2−2x+1 với trục hoành là
Cho hàm số y=x−23x−2 có đồ thị (C) và đường thẳng d:y=x+1.
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) (C) cắt trục hoành tại điểm có hoành độ x=2. |
|
| b) Đường tiệm cận ngang của đồ thị hàm số (C) là y=32. |
|
| c) Giao điểm của (C) với trục tung là N(0;−2). |
|
| d) Đường thẳng d cắt (C) tại hai điểm A và B thì tọa độ trung điểm M của đoạn thẳng AB là M(2;3). |
|
Cho hàm số y=f(x) có đồ thị là đường cong như hình vẽ:
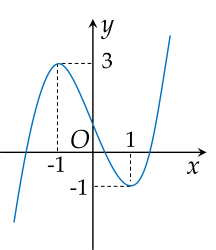
Số nghiệm của phương trình f(x)+2=0 là
Biết đường thẳng y=x−2 cắt đồ thị hàm số y=x−12x+1 tại hai điểm phân biệt A và B có hoành độ xA,xB. Giá trị của biểu thức xA+xB bằng
Đồ thị hàm số y=x−12x2−x−3 cắt trục hoành tại bao nhiêu điểm phân biệt?
Cho hàm số y=f(x)=x2+1. Số nghiệm của phương trình f(x+3)=1 là
Cho hàm số y=f(x) có bảng biến thiên như hình vẽ:
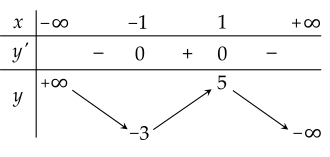
| a) Phương trình 2f(x)=5 có 3 nghiệm. |
|
| b) Hàm số đồng biến trên khoảng (−3;5). |
|
| c) Giá trị lớn nhất của hàm số trên [−1;2] bằng 1. |
|
| d) Hàm số đã cho có 2 cực trị. |
|
