Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Dạng 2. Thể tích khối tròn xoay SVIP
Yêu cầu đăng nhập!
Bạn chưa đăng nhập. Hãy đăng nhập để làm bài thi tại đây!
Cho hàm số y=f(x) liên tục trên đoạn [a;b]. Gọi D là hình phẳng giới hạn bởi đồ thị hàm số y=f(x), trục hoành và hai đường thẳng x=a, x=b. Thể tích khối tròn xoay tạo thành khi quay D quanh trục hoành được tính theo công thức nào?
Cho hình phẳng D giới hạn bởi đồ thị y=(2x−1)lnx, trục hoành và đường thẳng x=e.
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) Diện tích hình phẳng D=21∫1(2x−1)lnxdx. |
|
| b) Diện tích hình phẳng D=0∫e(2x−1)lnxdx. |
|
| c) Thể tích V khối tròn xoay tạo thành khi quay hình phẳng D quanh trục Ox: V=π1∫e(2x−1)2lnxdx. |
|
| d) Thể tích V khối tròn xoay tạo thành khi quay hình phẳng D quanh trục Ox: V=π21∫e(2x−1)2lnxdx. |
|
Cho hình phẳng (H) giới hạn bởi các đường y=x+11,y=0,x=0,x=2. Quay hình phẳng (H) quanh trục hoành tạo nên một khối tròn xoay có thể tích bằng
Gọi D là phần hình phẳng giới hạn bởi các đường x=−1;y=0;y=x3. Thể tích khối tròn xoay tạo nên khi quay D quanh trục Ox bằng
Hình phẳng (H) giới hạn bởi các đường y=x2+1, trục tung và tiếp tuyến của đồ thị hàm số y=x2+1 tại điểm (1;2). Khi quay hình (H) quanh trục Ox tạo thành khối tròn xoay có thể tích V bằng
Cho hàm số y=f(x)=ax3+bx2+cx+d(a,b,c,d∈R) có đồ thị (C). Biết rằng đồ thị (C) tiếp xúc với đường thẳng y=4 tại điểm có hoành độ âm và đồ thị hàm số y=f′(x) cho bởi hình vẽ dưới đây:
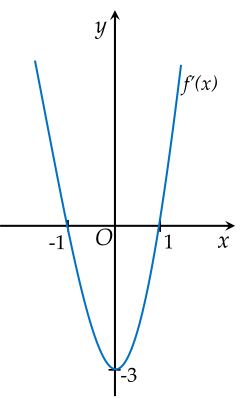
| a) Hàm số y=f(x) có điểm cực tiểu tại x=0. |
|
| b) Hàm số y=f(x) nghịch biến trên khoảng (−1;1) |
|
| c) Hàm số y=f(x)=x3−3x−2. |
|
| d) Thể tích vật thể tròn xoay được tạo thành khi quay hình phẳng H giới hạn bởi đồ thị (C) và trục hoành khi quay xung quanh trục Ox là 35729π |
|
Cho hàm số y=f(x) liên tục và có đồ thị như hình bên. Gọi D là hình phẳng giới hạn bởi đồ thị hàm số đã cho và trục Ox. Quay hình phẳng D theo trục Ox ta được khối tròn xoay có thể tích V được xác định bởi công thức

Thể tích của khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi đồ thị hàm số y=tanx, trục hoành và các đường thẳng x=0, x=4π quanh trục hoành là
Cho đồ thị hàm số y=ex và hình được tô màu như dưới

| a) Hình phẳng được tô màu giới hạn bởi ba đường. |
|
| b) Diện tích hình phẳng được tính bởi công thức S=−1∫1(ex)2dx. |
|
| c) Diện tích hình phẳng S=e−e1. |
|
| d) Thể tích khối tròn xoay khi quay hình phẳng đó quanh trục Ox là V=21π(e2−e21). |
|
Cho hình phẳng (H) giới hạn bởi các đường y=x2+3, y=0, x=0, x=2. Thể tích khối tròn xoay sinh ra khi quay hình phẳng (H) xung quanh trục Ox bằng baπ. Giá trị của a+b là
Trả lời:
