Lý thuyết và phương pháp giải Các phép toán với vectơ trong không gian

Câu 1 (1đ):

Cho hình lăng trụ $A B C . A' B' C', \, M$ là trung điểm của $B B'$ . Đặt $\overrightarrow{C A}=\overrightarrow{a}, \, \overrightarrow{C B}=\overrightarrow{b}, \, \overrightarrow{A A'}=\overrightarrow{c}$ . Khẳng định nào sau đây đúng?

\overrightarrow{A M}=\overrightarrow{a}-\overrightarrow{c}+\dfrac{1}{2} \overrightarrow{b}

.

\overrightarrow{A M}=\overrightarrow{b}-\overrightarrow{a}+\dfrac{1}{2} \overrightarrow{c}

.

\overrightarrow{A M}=\overrightarrow{a}+\overrightarrow{c}-\dfrac{1}{2} \overrightarrow{b}

.

\overrightarrow{A M}=\overrightarrow{b}+\overrightarrow{c}-\dfrac{1}{2} \overrightarrow{a}

.

Câu 2 (1đ):

Cho hình chóp $S . A B C D$ có đáy $A B C D$ là hình bình hành. Đặt $\overrightarrow{S A}=\overrightarrow{a} ; \, \overrightarrow{S B}=\overrightarrow{d} ; \, \overrightarrow{S C}=\overrightarrow{c}$ ; $\overrightarrow{S D}=\overrightarrow{b}$ . Khẳng định nào sau đây đúng?

\overrightarrow{a}+\overrightarrow{b}=\overrightarrow{c}+\overrightarrow{d}

.

\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}+\overrightarrow{d}=\overrightarrow{0}

.

\overrightarrow{a}+\overrightarrow{d}=\overrightarrow{b}+\overrightarrow{c}

.

\overrightarrow{a}+\overrightarrow{c}=\overrightarrow{d}+\overrightarrow{b}

.

Câu 3 (1đ):

Cho hình lập phương $A B C D . A_{1} B_{1} C_{1} D_{1}$ có tâm $O$ . Đẳng thức nào sau đây đúng?

\overrightarrow{A O}=\dfrac{2}{3}\left(\overrightarrow{A B}+\overrightarrow{A D}+\overrightarrow{A A_{1}}\right)

.

\overrightarrow{A O}=\dfrac{1}{3}\left(\overrightarrow{A B}+\overrightarrow{A D}+\overrightarrow{A A_{1}}\right)

.

\overrightarrow{A O}=\dfrac{1}{2}\left(\overrightarrow{A B}+\overrightarrow{A D}+\overrightarrow{A A_{1}}\right)

.

\overrightarrow{A O}=\dfrac{1}{4}\left(\overrightarrow{A B}+\overrightarrow{A D}+\overrightarrow{A A_{1}}\right)

.

Câu 4 (1đ):

Gọi $I$ là trung điểm của $AB$ và điểm $M$ bất kì khác $I$ , $A$ , $B$ . Khẳng định nào sau đây sai?

\overrightarrow{IA}=\overrightarrow{IB}

.

\overrightarrow{MA}+\overrightarrow{MB}=2\overrightarrow{MI}

.

IA=IB

.

\overrightarrow{IA}+\overrightarrow{IB}=\overrightarrow{0}

.

Câu 5 (1đ):

Trong không gian cho ba điểm $M,\,N,\,P$ phân biệt. Tổng $\overrightarrow{PM}+\overrightarrow{MN}$ là

\overrightarrow{MN}

.

\overrightarrow{NP}

.

\overrightarrow{NM}

.

\overrightarrow{PN}

.

Câu 6 (1đ):

Cho hình lập phương $ABCD.{A}'{B}'{C}'{D}'$ . Vectơ nào sau đây có điểm đầu và điểm cuối là đỉnh của hình lập phương $ABCD.{A}'{B}'{C}'{D}'$ và bằng $\overrightarrow{AD}$ ?

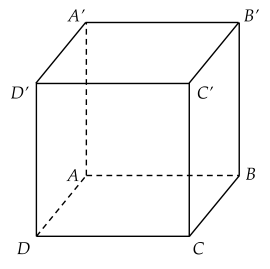
loading...

\overrightarrow{CB}

.

\overrightarrow{{B}'{C}'}

.

\overrightarrow{AB}

.

\overrightarrow{DA}

.

Câu 7 (1đ):

Cho hình hộp $ABCD.EFGH$ . Khi đó $\overrightarrow{AB}-\overrightarrow{EH}$ là

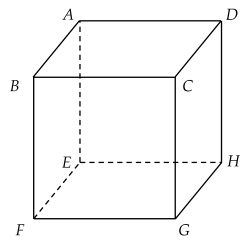
loading...

\overrightarrow{BD}

.

\overrightarrow{EG}

.

\overrightarrow{BH}

.

\overrightarrow{DB}

.

Câu 8 (1đ):

Cho tứ diện $ABCD$ . Gọi $G$ là trọng tâm tam giác $ABC.$ Giá trị của $k$ thích hợp điền vào đẳng thức vectơ $\overrightarrow{DA}+\overrightarrow{DB}+\overrightarrow{DC}=k\overrightarrow{DG}$ là

k=\dfrac{1}{3}

.

k=\dfrac{1}{2}

.

k=2.

k=3.

Câu 9 (1đ):

Cho hình hộp $ABCD.{A}'{B}'{C}'{D}'$ , có đáy $ABCD$ hình bình hành tâm $O$ .

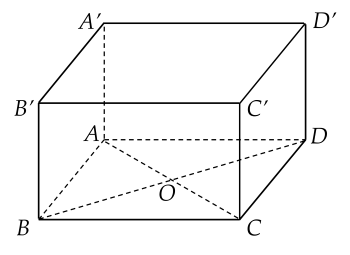
loading...

Khi đó $2\overrightarrow{AO}$ bằng vectơ nào dưới đây?

\overrightarrow{{A}'C}

.

\overrightarrow{AC}

.

\overrightarrow{AD}

.

\overrightarrow{AB}

.

Câu 10 (1đ):

Trong không gian $Oxyz$ , cho $\overrightarrow{u}=\left( 1;-1;4 \right)$ và $\overrightarrow{v}=\left( 3;-2;1 \right)$ . Khi đó $\overrightarrow{u}.\overrightarrow{v}$ bằng

9

.

7

.

-3

.

-9

.

Câu 11 (1đ):

Cho hình lập phương $ABCD.EFGH$ có cạnh bằng $5$ . Giá trị của $\overrightarrow{AB} . \overrightarrow{EG}$ là

125

.

25

.

\dfrac{5\sqrt3}3

.

5

.

Câu 12 (1đ):

Cho hai vectơ $\overrightarrow{u},\overrightarrow{v}$ có $| \overrightarrow{u} |=3,\,| \overrightarrow{v} |=4$ và góc giữa hai vectơ $\overrightarrow{u},\overrightarrow{v}$ bằng $60^\circ$ . Tích vô hướng $\overrightarrow{u}.\overrightarrow{v}$ bằng

-6

.

12

.

-12

.

6

.

Câu 13 (1đ):

Trong không gian cho hình lập phương $ABCD.{A}'{B}'{C}'{D}'$ có độ dài cạnh là $a$ . Gọi $O$ là giao điểm của $BD$ và $AC$ .

loading...

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) $\overrightarrow{{A}'C}-\overrightarrow{{A}'A}=\overrightarrow{AB}+\overrightarrow{AD}$ .
b) $\overrightarrow{B{C}'}=\overrightarrow{{A}'A}+\overrightarrow{{B}'{C}'}$ .
c) $\overrightarrow{{C}'O}=\overrightarrow{{C}'{A}'}-\overrightarrow{O{A}'}$ .
d) $\overrightarrow{{A}'D}.\overrightarrow{{A}'B}=0$ .

Câu 14 (1đ):

Cho hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$ thỏa mãn $| \overrightarrow{a}|=2$ ; $| \overrightarrow{b}|=5$ , góc giữa hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$ bằng $60^\circ$ .

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) $(\overrightarrow{a},\,-2\overrightarrow{b})=60^\circ$ .
b) $\overrightarrow{a}.\overrightarrow{b}=5$ .
c) $\| \overrightarrow{a}-2\overrightarrow{b}\|=84$ .
d) Biết vectơ $\overrightarrow{v}$ ngược hướng với vectơ $\overrightarrow{a}-2\overrightarrow{b}$ và $\| \overrightarrow{v} \|=4\sqrt{21}$ . Gọi $\alpha$ là góc giữa hai vectơ $\overrightarrow{v}$ và $\overrightarrow{a}$ . Khi đó $\cos \alpha =\dfrac{\sqrt{21}}{84}$ .

Câu 15 (1đ):

Cho tứ diện $ABCD$ có $AB\,=\,AC=AD=BC=BD=a$ , $\Delta BCD$ vuông cân tại $B$ . Gọi $M$ , $N$ lần lượt là trung điểm các cạnh $AB$ , $CD$ .

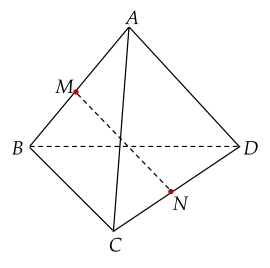
loading...

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) $\overrightarrow{AB}+\overrightarrow{DC}=\overrightarrow{AC}+\overrightarrow{DB}$ .
b) $2\overrightarrow{MN}=\overrightarrow{AC}+\overrightarrow{BD}$ .
c) $\overrightarrow{AB}.\overrightarrow{BC}=\dfrac{1}{2}{a^2}$ .
d) $(\overrightarrow{AD},\overrightarrow{BC})=120^\circ$ .

Bài học cùng chủ đề

Dạng 2. Các phép toán với vectơ trong không gian SVIP

Yêu cầu đăng nhập!

Bài học cùng chủ đề

Báo cáo học liệu

Mua học liệu

Mua học liệu:

Số dư ví của bạn: 0 coin - 0 Xu

Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu

Để nhận Coin\Xu, bạn có thể:

Chi tiết xem tại đây

Thông tin của bạn

Dạng 2. Các phép toán với vectơ trong không gian SVIP

Yêu cầu đăng nhập!

Truy vết IP log

Báo lỗi câu hỏi

Các khóa học có thể bạn quan tâm

Yêu cầu VIP