Dạng 1. Ứng dụng hình học của tích phân để tính diện tích hình phẳng SVIP

Diện tích hình phẳng $\left(H \right)$ được giới hạn bởi đồ thị hàm số $y=f\left(x \right)$, trục hoành và hai đường thẳng $x=a,\,x=b$ $\left(a<b \right)$ (phần gạch chéo như hình vẽ) được tính theo công thức nào?

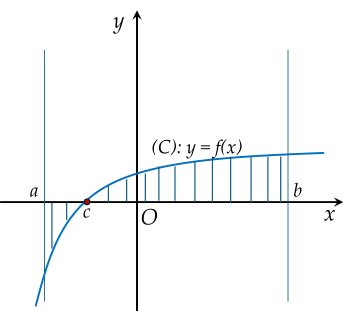
Diện tích hình phẳng giới hạn bởi đồ thị hàm số $y=\cos x$, trục tung, trục hoành và đường thẳng $x=\pi$ bằng$1$.

Cho đồ thị $y=f(x)$ như hình vẽ bên. Công thức diện tích miền được gạch sọc ở hình bên là

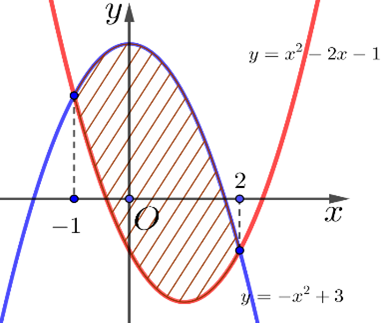
Gọi $S$ là diện tích của hình phẳng giới hạn bởi các đường $y=2^x$, $y=1$, $x=0$, $x=2$. Mệnh đề nào dưới đây sai?

Cho hàm số $y=f\left(x \right)$ và $y=g\left(x \right)$ có đồ thị như hình vẽ:

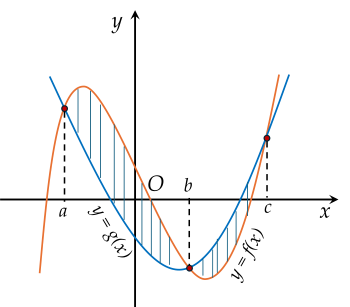
Diện tích $S$ của phần gạch chéo trong hình vẽ trên được tính bằng công thức là

Diện tích $S$ hình phẳng giới hạn bởi các đường $y=2{{x}^{2}}$, $y=-1$, $x=0$ và $x=1$ là

Diện tích của hình phẳng được giới hạn bởi đồ thị hàm số $y=f(x)$, trục hoành và hai đường thẳng $x=a$, $x=b$ ($a\lt b$) tính theo công thức nào dưới đây?

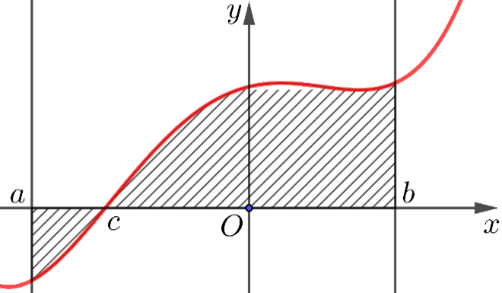
Một viên gạch đá hoa hình vuông cạnh $40$ cm được thiết kế như hình bên dưới. Diện tích mỗi cánh hoa bằng

Giá trị của $a$ để diện tích $S$ của hình phẳng giới hạn bởi $(P): y=\dfrac{x^2-2x}{x-1}$, đường thẳng $d: y=x-1$ và $x=a$,

$x=2a$ ($a>1$) bằng $\ln3$ là

Diện tích hình phẳng giới hạn bởi parabol $y={{x}^{2}}$ và đường thẳng $y=3x-2$ là