Cho hàm số bậc ba $y=f(x)$ có đồ thị như hình vẽ:

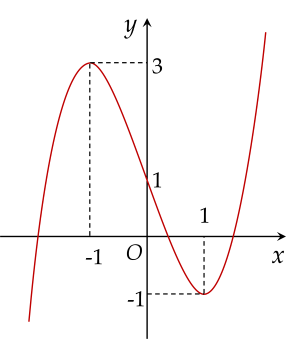
Trên đoạn $[0;1]$, hàm số $y = f(x)$ đạt giá trị nhỏ nhất tại

Giá trị lớn nhất, giá trị nhỏ nhất của hàm số $y={{x}^{4}}-2{{x}^{2}}+3$ lần lượt là

Gọi $M$, $m$ lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y = f\left( x \right)=\dfrac{2x-1}{x+1}$ trên đoạn $\left[ 0;3 \right]$. Giá trị $M-m$ bằng

Giá trị nhỏ nhất của hàm số $$y=\dfrac{x-1}{x+1}$$ trên đoạn $\left[ 0;3 \right]$ là

Giá trị lớn nhất và nhỏ nhất của hàm số $y=2{{x}^{3}}+3{{x}^{2}}-1$ trên đoạn $\left[ -2;\,1 \right]$ lần lượt là

Tích của giá trị nhỏ nhất và giá trị lớn nhất của hàm số $y = f\left( x \right)=x+\dfrac{4}{x}$ trên đoạn $\left[ 1;3 \right]$ bằng

Giá trị nhỏ nhất của hàm số $y=x^3-3x+5$ trên đoạn $\left[ 2;4 \right]$ là

Gọi $M, \, m$ lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số $y=\sqrt{5-4x}$ trên đoạn $\left[ -1;\,1 \right]$. Giá trị $M-m$ bằng

Giá trị lớn nhất của hàm số $y={{x}^{3}}-{{x}^{2}}-8x$ trên $\left[ 1;3 \right]$ là

Giá trị lớn nhất của hàm số $y=2x^3+3x^2-12x+2$ trên đoạn $\left[ -1;2 \right]$ là

Giá trị lớn nhất của hàm số $y = f(x)=x^3-3x^2-9x+10$ trên $\left[ -2;2 \right]$ là

Giá trị lớn nhất của hàm số $y=-x^4+4x^2$ trên đoạn $\left[ -1;2 \right]$ bằng

Giá trị nhỏ nhất của hàm số $y = f(x)=x^3+3x$ trên đoạn $\left[ -1;2 \right]$ bằng

Gọi $M$, $m$ lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y=\dfrac{x^2+5}{x-2}$ trên $\left[ -2;1 \right]$. Giá trị của $M+2m$ bằng

Giá trị lớn nhất của hàm số $y={{x}^{3}}-2{{x}^{2}}-7x+1$ trên đoạn $\left[ -2;1 \right]$ là