Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Con lắc đơn SVIP
I. Thế nào là con lắc đơn?
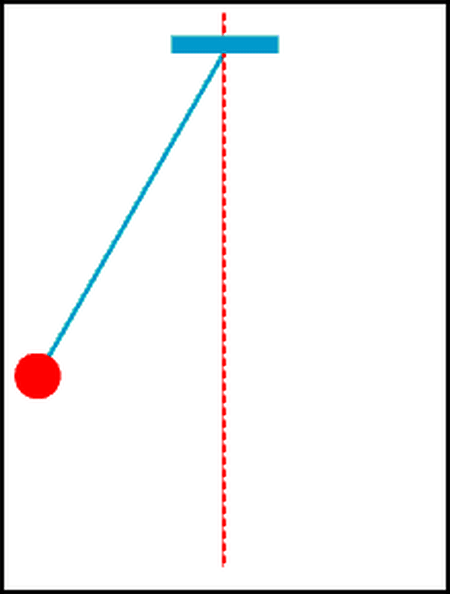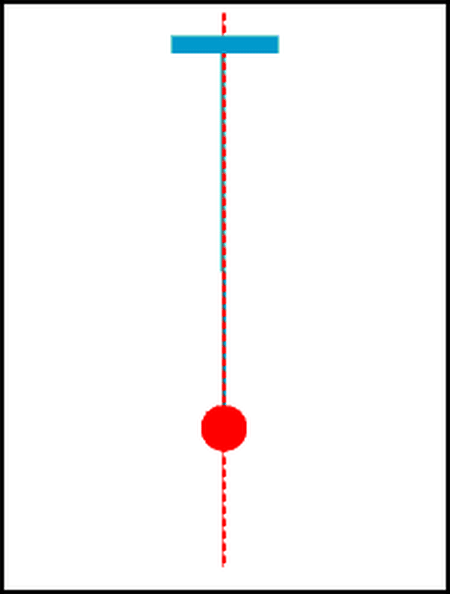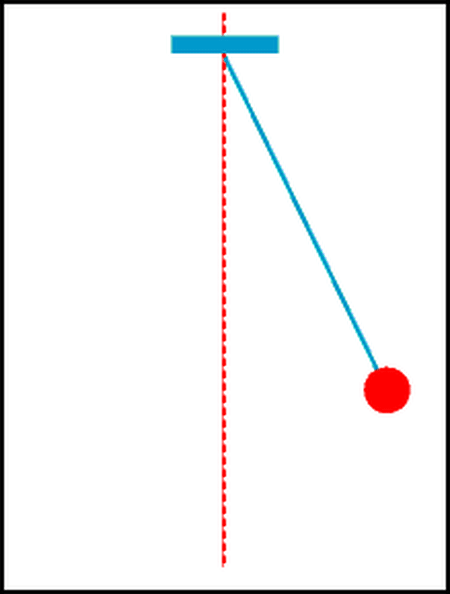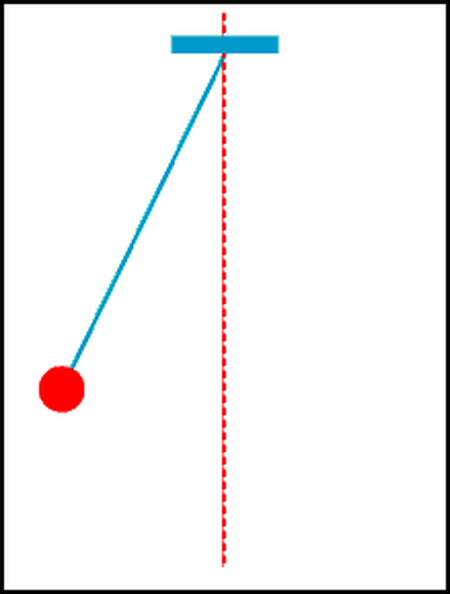
- Con lắc đơn gồm một vật nhỏ, khối lượng \(m\), được treo vào đầu một sợi dây không dãn, khối lượng không đáng kể, chiều dài \(l\).
- Vị trí cân bằng của con lắc là vị trí dây treo có phương thẳng đứng.
- Kéo nhẹ quả cầu cho dây treo lệch khỏi vị trí cân bằng một góc rồi thả ra, thấy con lắc dao động quanh vị trí cân bằng trong mặt phẳng thẳng đứng đi qua điểm treo và vị trí ban đầu của vật.
II. Khảo sát dao động của con lắc đơn về mặt động lực học

Trong khi dao động vật chịu tác dụng của:
- Trọng lực \(\overrightarrow{P}\)
- Lực căng dây \(\overrightarrow{T}\)
Lực thành phần \(\overrightarrow{P_t}\) là lực kéo về và có giá trị
\(P_t=-mg\sin\alpha\)
Nếu góc \(\alpha\) nhỏ thì \(\sin\alpha\approx\alpha\), do đó
\(P_t=-mg\dfrac{s}{l}\)
Vậy con lắc dao động điều hòa với phương trình
\(s=s_0\cos\left(\omega t+\varphi\right)\)
Chu kì dao động của con lắc là
\(T=2\pi\sqrt{\dfrac{l}{g}}\)
III. Khảo sát dao động của con lắc đơn về mặt năng lượng
 1. Động năng của con lắc đơn là động năng của vật
1. Động năng của con lắc đơn là động năng của vật
\(W_đ=\dfrac{1}{2}mv^2\)
2. Thế năng của con lắc đơn là thế năng trọng trường
\(W_t=mgh=mgl\left(1-\cos\alpha\right)\)
3. Cơ năng của con lắc đơn bằng tổng động năng và thế năng
\(W=\dfrac{1}{2}mv^2+mgl\left(1-\cos\alpha\right)\)
Nếu bỏ qua mọi ma sát thì cơ năng của con lắc được bảo toàn.
IV. Ứng dụng: Xác định gia tốc rơi tự do
_11.jpg)
Để đo gia tốc trọng trường tại một nơi nào đó trên bề mặt trái đất, người ta làm như sau:
- Dùng một con lắc đơn có chiều dài \(l\) tính đến tâm của quả cầu
- Đo thời gian của một số dao động toàn phần từ đó tính ra chu kì \(T\)
- Tính được gia tốc trọng trường theo công thức \(g=\dfrac{4\pi^2l}{T^2}\)
- Lặp lại thí nghiệm nhiều lần với các con lắc có chiều dài khác nhau, tính giá trị \(g\) và lấy trung bình
Bạn có thể đăng câu hỏi về bài học này ở đây
