Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Chứng minh hai đường thẳng vuông góc SVIP
Cho một điểm $O$ nằm trên đường thẳng $x x'$. Trên nửa mặt phẳng có bờ là $x x'$ dựng hai tia $O M$ và $O N$ sao cho $\widehat{x O M}=\widehat{N O x'}=30^{\circ}$. Gọi tia $O t$ là phân giác của $\widehat{M O N}$. Chứng minh $O t \perp x x'$.
Hướng dẫn giải:
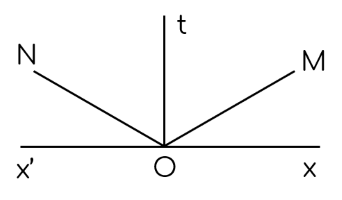
Tia $O t$ là phân giác của $\widehat{M O N}$ nên $\widehat{M O t}=\widehat{N O t}=\dfrac{1}{2} \widehat{M O N}$. (1)
Hai tia $O M$ và $O N$ cùng nằm trên nửa mặt phẳng bờ $x x'$ và tia $O t$ là phân giác của $\widehat{M O N}$ nên $O N$ nằm giữa $O x'$ và $O t$.
Suy ra $\widehat{x' O t}=\widehat{x' O \bar{N}}+\widehat{N O t}$. (2)
Từ (1) và (2), ta có $\widehat{x' O t}=\widehat{x' O N}+\widehat{M O t}$. (*)
$O M$ nằm giữa $O x$ và $O t$ nên $\widehat{x O t}=\widehat{x O M}+\widehat{M O t}$. (3)
Mặt khác $\widehat{x O M}=\widehat{x' O N}=30^{\circ}$. (4)
Từ (3) và (4), ta có $\widehat{x O t}=\widehat{x' O N}+\widehat{M O t}$ (* *)
Từ (*) và $(* *)$ suy ra $\widehat{x O t}=\widehat{x' O t}=\dfrac{1}{2} \widehat{x' O x}=\dfrac{1}{2}. 180^{\circ}=90^{\circ}$.
Vậy $O t \perp x' x$.
Cho $\widehat{x O y}=90^{\circ}$, vẽ hai tia $O A,$ $O B$ ở trong góc đó sao cho $\widehat{x O A}=\widehat{y O B}=60^{\circ}$. Trên nửa mặt phẳng bờ $O x$ chứa tia $O y$, vẽ tia $O M$ sao cho $O y$ là tia phân giác của $\widehat{M O B}$.
a) Chứng minh tia $O A$ là tia phân giác $\widehat{y O B}$, tia $O B$ là tia phân giác $\widehat{x O A}$.
b) Chứng minh $O M \perp O A$.
Hướng dẫn giải:
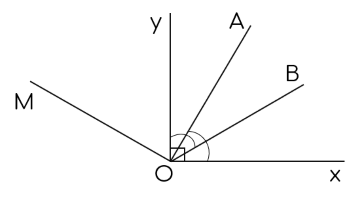
a) Vì $O A$ nằm trong góc $\widehat{x O y}$ nên tia $O A$ nằm giữa hai tia $O x,$ $O y$.
Suy ra $\widehat{x O y}=\widehat{x O A}+\widehat{A O y} \Rightarrow \widehat{A O y}=\widehat{x O y}-\widehat{x O A}=90^{\circ}-60^{\circ}=30^{\circ}$. (1)
Vì $O B$ nằm trong góc $\widehat{x O y}$ nên tia $O B$ nằm giữa hai tia $O x,$ $O y$.
Suy ra $\widehat{xO y}= \widehat{xO B}+\widehat{B O y} \Rightarrow \widehat{x O B}= \widehat{xO y}-\widehat{y O B}=90^{\circ}-60^{\circ}=30^{\circ}$ (2)
Trên cùng một nửa mặt phẳng bờ chứa tia $O x$ có $\widehat{x O B}<\widehat{x O A}$ (do $30^{\circ}<60^{\circ}$ ) nên tia $O B$ nằm giữa hai tia $O x$ và $O A$.
Suy ra $\widehat{x O A}=\widehat{x O B}+\widehat{A O B} \Rightarrow \widehat{A O B}=\widehat{x O A}-\widehat{x O B}=60^{\circ}-30^{\circ}=30^{\circ}$. (3)
Từ (2), (3) ta có $\widehat{x O B}=\widehat{A O B}$.
Mà tia $O B$ nằm giữa hai tia $O x$, $O A$ nên tia $O B$ là tia phân giác $\widehat{xO A}$.
Trên cùng một nửa mặt phẳng bờ chứa tia $O y$ có $\widehat{y O A}<\widehat{y O B}$ (do $30^{\circ}<60^{\circ}$ ) nên tia $O A$ nằm giữa hai tia $O y$ và $O B$.
Từ (1) và (3) suy ra $\widehat{y O A}=\widehat{A O B}$ nên $O A$ là tia phân giác $\widehat{y O B}$.
b) Ta có $\widehat{M O y}=\widehat{y O B}=60^{\circ}$ (do $O y$ là tia phân giác của $\widehat{M O B}$).
Suy ra $\widehat{M O B}=\widehat{M O y}+\widehat{y O B}=120^{\circ}$.
Trên cùng một nửa mặt phẳng bờ chứa tia $O B$ có $\widehat{M O B}>\widehat{A O B}$ (vì $120^{\circ}>30^{\circ})$ nên tia $O A$ nằm giữa hai tia $OM$ và $OB$.
$\Rightarrow \widehat{M O B} = \widehat{M O A} + \widehat{A O B} \Rightarrow \widehat{A O M} = \widehat{M OB} + \widehat{A O B} = 120^{\circ} - 30^{\circ} = 90^{\circ}$.
Vậy $OM \perp OA$.
Cho góc $\widehat{x O y}=140^{\circ}$. Ở ngoài của góc, vẽ hai tia $O A$ và $O B$ sao cho $O A \perp O x,$ $O B \perp O y$. Gọi $O M$ là tia phân giác của $\overline{x O y}$ và $O M'$ là tia đối của tia $OM$.
a) Chứng minh $O M'$ là tia phân giác của $\widehat{A O B}$.
b) Tính số đo góc $\widehat{xOB}$.
Hướng dẫn giải:
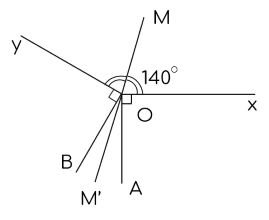
a) Ta có $\widehat{x O y}=140^{\circ}$ (giả thiết), $\widehat{x O A}=\widehat{y O B}=90^{\circ}$ (do $O A \perp O x,$ $O B \perp O y$).
$O M'$ là tia đối của $O M \Rightarrow \widehat{MOM}'=180^{\circ}$.
Mà $O A$ nằm ngoài góc $\widehat{xO y}$ và $O A \perp O x$ nên $\widehat{M OM'}=\widehat{M O x}+\widehat{xO A}+\widehat{A O M'}$.
Do đó $\widehat{A O M'}=\widehat{M OM'}-(\widehat{M O x}+\widehat{x O A}) \Rightarrow \widehat{A OM'}=180^{\circ}-\left(70^{\circ}+90^{\circ}\right)=20^{\circ}$.
Mặt khác $O y$ nằm giữa $O B$ và ${OM}$ nên $\widehat{M O B}=\widehat{M O y}+\widehat{y O B}=70^{\circ}+90^{\circ}=160^{\circ}$.
$\Rightarrow \widehat{M O B}<\widehat{M O M'}$.
Do đó tia $O B$ và $O y$ nằm cùng nửa mặt phẳng bờ $MM'$.
${Ox}$ nằm giữa ${OA}$ và ${OM}$ nên $\widehat{M O A}=\widehat{M O x}+\widehat{xO A}=70^{\circ}+90^{\circ}=160^{\circ}$.
$\Rightarrow \widehat{M O A}<\widehat{M O M'}$.
Do đó tia $O A$ và $O x$ nằm cùng nửa mặt phẳng bờ $M M'$.
Nên $O M'$ nằm giữa $O A$ và $O B$.
$\Rightarrow \widehat{A O B}=\widehat{A O M'}+\widehat{M' O B} \Rightarrow \widehat{M' O B}=\widehat{A O B}-\widehat{A O M'}=40^{\circ}-20^{\circ}=20^{\circ}$ (2)
Từ (1) và (2) ta có $\widehat{M}' \widehat{O B}=\widehat{A O M} \widehat{M'}=20^{\circ}=\dfrac{1}{2} \widehat{AO B}$.
Suy ra $O M'$ là tia phân giác của góc $\widehat{A O B}$.
b) Ta có $\widehat{M O x}<\widehat{M O A}<\widehat{M O M}$ nên $O A$ nằm giữa $O x$ và $O M'$.
Mà $O M'$ là tía phân giác của góc $\widehat{A O B}$.
Suy ra $O A$ nằm giữa $O x$ và $O B$.
Vậy $\widehat{xO B}=\widehat{xO A}+\widehat{A O B}=90^{\circ}+40^{\circ}=130^{\circ}$.
