BIỂU DIỄN THẬP PHÂN CỦA SỐ HỮU TỈ SVIP

I. SỐ THẬP PHÂN HỮU HẠN VÀ SỐ THẬP PHÂN VÔ HẠN TUẦN HOÀN

*Đặt tính để tìm thương của 

Nhận xét:

• Số thập phân \(1,92\) chỉ có hai chữ số sau dấu ",".
• Các số thập phân chỉ gồm hữu hạn số sau dấu "," được gọi là số thập phân hữu hạn.

*Đặt tính để tìm thương của 

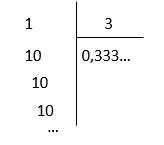
Nhận xét: Phép chia này không bao giờ chấm dứt. Nếu cứ tiếp tục chia thì phần thập phân của thương, chữ số \({}\) sẽ xuất hiện liên tiếp mãi. Ta nói rằng khi chia \({}\)\(1\) cho \(3\) , ta được số \(0,333...\) đó là số thập phân vô hạn tuần hoàn.

*Nhận xét: Các số thập phân vô hạn tuần hoàn \(0,333...;\) \(1,8333...\); \(2,4646...\)có tính chất: Trong phần thập phân, bắt đầu từ một hàng nào đó, có một chữ số hay một cụm chữ số liền nhau xuất hiện liên tiếp mãi, phần xuất hiện mãi đó người ta gọi là chu kì của số thập phân vô hạn đó.

Ví dụ:(1) Trong phần thập phân của số \(0,333...\), chữ số 3 xuất hiện liên tiếp mãi bắt đầu từ hàng phần mười. Số \(3\) được gọi là chu kì của số thập phân vô hạn tuần hoàn \(0,333...\)Và số thập phân đó viết gọn là \(0,\left(3\right)\).

(2)Tương tự, \(3\) là chu kì của số thập phân vô hạn tuần hoàn \(1,8333...\) và \(1,8333...=1,8\left(3\right).\)

(3) Ta thấy \(46\) là chu kì của số thập phân vô hạn tuần hoàn \(2,4646...\) và \(2,4646...=2,\left(46\right)\).

II. BIỂU DIỄN THẬP PHÂN CỦA SỐ HỮU TỈ

Nhận xét: Mỗi số hữu tỉ được biểu diễn bởi một số thập phân hữu hạn hoặc vô hạn tuần hoàn.