Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Bài toán liên quan đến hai đường tròn tiếp xúc nhau SVIP
Cho hai đường tròn $(O)$ và $(O')$ tiếp xúc ngoài tại $A$. Kẻ các đường kính $AOB$, $AO'C$. Gọi $DE$ là tiếp tuyến chung của hai đường tròn. Gọi $M$ là giao điểm của $BD$ và $CE$.
a. Tính số đo $\widehat{DAE}$.
b. Tứ giác $ADME$ là hình gì? Vì sao?
c. Chứng minh rằng $MA$ là tiếp tuyến chung của hai đường tròn.
Hướng dẫn giải:
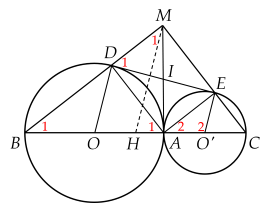
a) Ta có: $\widehat{A_1}=(180^\circ-\widehat{O_1}) \, : \, 2$
$\widehat{A_2}=(180^\circ-\widehat{O_2}) \, : \, 2$
Suy ra $\widehat{A_1}+\widehat{A_2}=90^\circ$ suy ra $\widehat{DAE}=90^\circ$.
b) Có tứ giác $ADME$ là hình chữ nhật (tứ giác có ba góc vuông là hình chữ nhật).
c) Gọi $I$ là giao điểm của $DE$ và $AM$ suy ra $ID=IA$
$\Delta IAO=\Delta IDO$ (ccc) suy ra $\widehat{IAO}=\widehat{IDO}=90^\circ$
Suy ra $MA \bot OA$ với $A \in (O)$
Chứng minh tương tự: $MA \bot O'A$ với $A \in (O')$.
Vậy $MA$ là tiếp tuyến chung của hai đường tròn.
Cho ba điểm $J, \, I, \, J'$ cùng nằm trên một đường thẳng theo thứ tự đó. Cho biết $IJ=10$ cm, $IJ'=4$ cm. Vẽ đường tròn $(O)$ đường kính $IJ$ và đường tròn $(O')$ đường kính $IJ'$.
a. Chứng minh $(O)$ và $(O')$ tiếp xúc ngoài ở $I$.
b. Gọi $A$ là điểm trên đường tròn $(O)$, tia $AI$ cắt $(O')$ ở $A'$. Chứng minh rằng $\Delta AIJ\backsim\Delta A'IJ'$.
c. Qua điểm $I$ kẻ cát tuyến cắt $(O)$ ở $B$ ($B$ và $A$ thuộc hai nửa mặt phẳng bờ $IJ$), cắt đường tròn $(O')$ ở $B'$. Chứng minh $\Delta IAB\backsim\Delta IA'B'$.
d. Chứng minh rằng: $\Delta OAB \backsim \Delta OA'B'$.
e. Tứ giác $ABA'B'$ là hình gì?
Hướng dẫn giải:
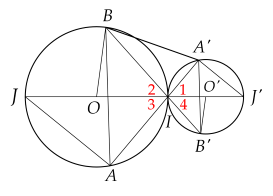
a) Ta có: $OO'=OI+O'I$.
Vậy hai đường tròn tiếp xúc ngoài tại $I$.
b) Xét $\Delta AIJ$ và $\Delta A'IJ'$ có:
$\widehat{A}=\widehat{A'}=90^\circ$
$\widehat{I_1}=\widehat{I_2}$ suy ra $\Delta AII \backsim \Delta A'IJ'$.
c) $\Delta AIJ \backsim\Delta A'IJ'$ (g.g)
Suy ra $\dfrac{IA}{IA'}=\dfrac{IJ}{JI'}=\dfrac{10}{4}=\dfrac{5}{2}$ (1)
$\Delta OIB \backsim \Delta O'IB'$ (g.g) suy ra $OB$ // $O'B'$
Suy ra $\widehat{B_1}=\widehat{B'_1}$ suy ra $\dfrac{IB}{IB'}=\dfrac{OB}{O'B'}=\dfrac{5}{2}$ (2)
Từ (1) và (2) suy ra $\dfrac{IA}{IA'}=\dfrac{IB}{IB'}=\dfrac{5}{2}$; $\widehat{AIB}=\widehat{A'IB}$
Nên $\Delta IAB \backsim \Delta IA'B'$ (c.g.c).
d) $\Delta IAB \backsim \Delta IA'B'$ (c.g.c)
Suy ra $\dfrac{AB}{A'B'}=\dfrac{IA}{IA'}=\dfrac{5}{2}$;
$\dfrac{OA}{O'A'}=\dfrac{OB}{O'B'}=\dfrac{5}{2}$
Suy ra $\dfrac{OA}{O'A'}=\dfrac{OB}{O'B'}=\dfrac{AB}{A'B'}$ suy ra $\Delta AOB\backsim \Delta A'O'B'$ (c.c.c).
e) $\Delta AOB\backsim\Delta A'O'B'$ suy ra $\widehat{OBA}=\widehat{O'B'A'}; \, \widehat{OBI}=\widehat{O'B'I'}$
Suy ra $\widehat{ABI}=\widehat{AB'I'}$ nên $AB$ // $A'B'$.
Tứ giác $ABA'B'$ có hai cạnh đối song song nên nó là hình thang.
Cho hai đường tròn $(O ; R)$ và $(O' ; r)$ tiếp xúc với nhau tại $A$. Vẽ một cát tuyến qua $A$ cắt hai đường tròn tại $B$ và $C$. Chứng minh rằng các tiếp tuyến tại $B$ và $C$ song song với nhau.
Hướng dẫn giải:
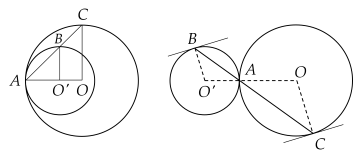
Trường hợp 1: $(O)$ và $(O')$ tiếp xúc trong.
Xét $\Delta OAC$, ta có:
$\dfrac{O'B}{OC}=\dfrac{r}{R}=\dfrac{O'A}{OA}$ suy ra $O'B$ // $OC$.
Suy ra các tiếp tuyến tại $B$ và $C$ song song với nhau vì chúng lần lượt vuông góc với $O'B$ và $OC$.
Trường hợp 2: $(O)$ và $(O')$ tiếp xúc ngoài.
Ta thấy $\Delta O'AB \backsim \Delta OAC$ (g.g)
Suy ra $\dfrac{O' B}{OC}=\dfrac{r}{R}=\dfrac{O'A}{OA}$
Nên $O'B$ // $OC$.
Lập luận tương tự như trên, ta được điều phải chứng minh.
Cho đường tròn tâm $O$ bán kính $OA$ và đường tròn đường kính $OA$.
a) Xác định vị trí tương đối của hai đường tròn.
b) Dây $AD$ của đường tròn lớn cắt đường tròn nhỏ ở $C$. Chứng minh rằng $AC = CD$.
Hướng dẫn giải:
a) Gọi $(O')$ là đường tròn đường kính $OA$.
Vì $OO'=OA-O'A$ nên hai đường tròn $(O)$ và $(O')$ tiếp xúc trong.
b) Các tam giác cân $AO'C$ và $AOD$ có chung góc ở đỉnh $A$ nên $\widehat{ACO'}=\widehat{D}$, suy ra $O'C$ // $OD$.
Tam giác $AOD$ có $AO'=O'O$ và $O'C$ // $OD$ nên $AC=CD$.
