Bài học cùng chủ đề
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Vận dụng được đạo hàm và khảo sát hàm số để giải quyết vấn đề thực tiễn SVIP
Định luật vạn vật hấp dẫn của Newton được cho bởi công thức F=Gr2m1.m2. Trong đó F là lực hấp dẫn giữa hai vật thể bất kì, G là hằng số hấp dẫn, m1,m2 là khối lượng các vật, r là khoảng cách giữa chúng. Đồ thị của hàm số cho bởi công thức này có tiệm cận đứng là r=0, điều này có nghĩa là khi r dần về 0 thì lực hấp dẫn sẽ tiến đến
Số dân của một thị trấn sau t năm kể từ năm 1970 được ước tính bởi công thức f(t)=t+526t+10;f(t) được tính bằng nghìn người. Xem f(t) là một hàm số xác định trên nửa khoảng [0;+∞). Đồ thị hàm số y=f(t) có đường tiệm cận ngang là y=a. Giá trị của a là
Giả sử một hạt chuyển động trên một trục thẳng đứng chiều dương hướng lên trên sao cho toạ độ của hạt (đơn vị: mét) tại thời điểm t (giây) là y=t3−12t+3,t≥0.
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) Hàm vận tốc là: v(t)=3t2−12,t≥0. |
|
| b) Hạt chuyển động xuống dưới khi t>2. |
|
| c) Quãng đường hạt đi được trong khoảng thời gian 0≤t≤3 là 9 m. |
|
| d) Khi t>0 thì hạt tăng tốc. |
|
Trong 200 gam dung dịch muối nồng độ 15%, giả sử thêm vào dung dịch x (gam) muối tinh khiết và được dung dịch có nồng độ f(x)%.
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) Hàm số f(x)=x+30100(x+200). |
|
| b) Đạo hàm của hàm số luôn nhận giá trị âm trên khoảng (0;+∞). |
|
| c) Thêm càng nhiều gam muối tinh khiết thì nồng độ phần trăm càng tăng và không vượt quá 100%. |
|
| d) Tiệm cận ngang của đồ thị hàm số y=f(x) là y=100. |
|
Một cơ sở sản xuất khăn mặt đang bán mỗi chiếc khăn với giá 30000 đồng một chiếc và mỗi tháng cơ sở bán được trung bình 3000 chiếc khăn. Cơ sở sản xuất đang có kế hoạch tăng giá bán để có lợi nhận tốt hơn. Sau khi tham khảo thị trường, người quản lý thấy rằng nếu từ mức giá 30000 đồng mà cứ tăng giá thêm 1000 đồng thì mỗi tháng sẽ bán ít hơn 100 chiếc. Biết vốn sản xuất một chiếc khăn không thay đổi là 18000 đồng.
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) Để đạt lợi nhuận lớn nhất thì mỗi chiếc khăn cần tăng thêm 10000 đồng. |
|
| b) Để đạt lợi nhuận lớn nhất thì mỗi chiếc khăn cần bán với giá 39000 đồng. |
|
| c) Để đạt lợi nhuận lớn nhất thì sau khi tăng giá mỗi chiếc khăn lãi 21000 đồng. |
|
| d) Để đạt lợi nhuận lớn nhất thì số khăn bán ra giảm 800 chiếc. |
|
Khi nuôi cá thí nghiệm trong hồ, một nhà sinh vật học thấy rằng: Nếu trên mỗi đơn vị diện tích của mặt hồ có n con cá thì trung bình mỗi con cá sau một vụ cân nặng P(n)=480−20n. Số con cá phải thả trên một đơn vị diện tích của mặt hồ để sau một vụ thu hoạch được nhiều gam cá nhất là bao nhiêu?
Trả lời:
Một cơ sở sản xuất khăn mặt đang bán mỗi chiếc khăn với giá 30000 đồng một chiếc và mỗi tháng cơ sở bán được trung bình 3000 chiếc khăn. Cơ sở sản xuất đang có kế hoạch tăng giá bán để có lợi nhận tốt hơn. Sau khi tham khảo thị trường, người quản lý thấy rằng nếu từ mức giá 30000 đồng mà cứ tăng giá thêm 1000 đồng thì mỗi tháng sẽ bán ít hơn 100 chiếc. Biết vốn sản xuất một chiếc khăn không thay đổi là 18000. Cơ sở sản xuất phải bán với giá mới là bao nhiêu nghìn đồng để đạt lợi nhuận lớn nhất?
Trả lời:
Cho hai vị trí A, B cách nhau 615 m, cùng nằm về một phía bờ sông như hình vẽ. Khoảng cách từ A và từ B đến bờ sông lần lượt là 118 m và 487 m. Một người đi từ A đến bờ sông để lấy nước mang về B. Đoạn đường ngắn nhất mà người đó có thể đi khoảng bao nhiêu mét? (kết quả làm tròn đến hàng đơn vị của mét)

Trả lời:
Đường dây điện 110KV kéo từ trạm phát (điểm A) trong đất liền ra Côn Đảo (điểm C). Biết khoảng cách ngắn nhất từ C đến B là 60 km, khoảng cách từ A đến B là 100 km, mỗi km dây điện dưới nước chi phí là 5 nghìn USD, chi phí cho mỗi km dây điện trên bờ là 3 nghìn USD. Điểm G cách B bao nhiêu km để mắc dây điện từ A đến G rồi từ G đến C chi phí là ít nhất?
Trả lời:
Một công ty muốn làm một đường ống dẫn từ một điểm A trên bờ đến một điểm B trên một hòn đảo. Hòn đảo cách bờ biển 6 km. Giá để xây đường ống trên bờ là 50000 USD mỗi km, và 130000 USD mỗi km để xây dưới nước. B′ là điểm trên bờ biển sao cho B′B vuông góc với bờ biển. Khoảng cách từ A đến B′ là 9 km. Vị trí C trên đoạn AB′ sao cho khi nối ống theo ACB thì số tiền ít nhất. Khi đó C cách A một đoạn bằng bao nhiêu ki-lô-mét? (kết quả ghi dưới dạng số thập phân)

Trả lời:
Một cửa hàng bán lẻ bán 2500 cái ti vi mỗi năm. Chi phí giữ trong kho là 10$ một cái mỗi năm. Để đặt hàng chi phí cố định cho mỗi lần đặt là 20$ cộng thêm 9$ mỗi cái. Mỗi năm cửa hàng nên đặt bao nhiêu cái ti vi để chi phí hàng tồn kho là nhỏ nhất?
Trả lời:
Một xưởng in có 8 máy in, mỗi máy in được 4000 bản in khổ giấy A4 trong một giờ. Chi phí để bảo trì, vận hành một máy trong mỗi lần in là 50000 đồng. Chi phí in ấn của n máy chạy trong một giờ là 20(3n+5) nghìn đồng. Nếu in 50000 bản in khổ giấy A4 thì phải sử dụng bao nhiêu máy để thu được nhiều lãi nhất?
Trả lời:
Một bức tường cao 2 m nằm song song với tòa nhà và cách tòa nhà 2 m.

Người ta muốn chế tạo một chiếc thang bắc từ mặt đất bên ngoài bức tường, gác qua bức tường và chạm vào tòa nhà. Chiều dài tối thiểu của thang bằng bao nhiêu mét? Làm tròn kết quả đến chữ số hàng phần trăm
Trả lời:
Người ta muốn mạ vàng cho một cái hộp có đáy hình vuông không nắp có thể tích là 4 lít. Giả sử độ dày của lớp mạ tại mọi nơi trên mặt ngoài hộp là như nhau. Kích thước của hộp đó với cạnh đáy bằng x dm và chiều cao h dm thì lượng vàng dùng để mạ là ít nhất. Tính a+b.
Trả lời:
Một con thuyền đang ở ngoài khơi cách đất liền 120 km và cách hòn đảo 450 km. Hòn đảo cách đất liền 270 km. Con thuyền cần cập bến để tiếp nhiên liệu rồi mang quà Tết ra đảo.

Quãng đường ngắn nhất mà con thuyền đó đi là bao nhiêu km?
Trả lời:
Giả sử doanh số (tính bằng số sản phẩm) của một sản phẩm mới (trong vòng một số năm nhất định) tuân theo quy luật logistic được mô hình hoá bằng hàm số y=f(t)=1+5e−t5000,t≥0, trong đó thời gian t (năm) được tính kể từ khi phát hành sản phẩm mới. Khi đó, đạo hàm f′(t) sẽ biểu thị tốc độ bán hàng. Sau khi phát hành bao nhiêu năm thì tốc độ bán hàng là lớn nhất? (làm tròn kết quả tới chữ số hàng phần mười)
Trả lời:
Từ một miếng tôn có hình dạng là một nửa hình tròn bán kính R=3, người ta cắt ra một miếng hình chữ nhật MNPQ như mô tả trong hình vẽ.
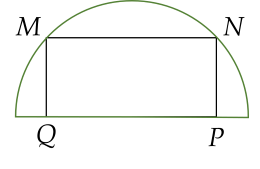
Diện tích lớn nhất có thể có của hình chữ nhật nêu trên là bao nhiêu (đơn vị diện tích)? (Làm tròn kết quả đến chữ số hàng đơn vị)
Trả lời:
Người quản lí của một khu chung cư có 100 căn hộ cho thuê nhận thấy rằng tất cả các căn hộ sẽ có người thuê nếu giá thuê một căn hộ là 8 triệu đồng một tháng. Một cuộc khảo sát thị trường cho thấy rằng, trung bình cứ mỗi lần tăng giá thuê căn hộ thêm 100 nghìn đồng thì sẽ có thêm một căn hộ bị bỏ trống. Người quản lí nên đặt giá thuê mỗi căn hộ là bao nhiêu để doanh thu là lớn nhất? (đơn vị: triệu đồng)
Trả lời:
Trong bài thực hành của môn huấn luyện quân sự có tình huống chiến sĩ phải bơi qua một con sông để tấn công một mục tiêu ở phía bờ bên kia sông. Biết rằng lòng sông rộng 100 m và vận tốc bơi của chiến sĩ bằng một nửa vận tốc chạy trên bờ. Nếu như dòng sông là thẳng, mục tiêu ở cách chiến sĩ 1 km theo đường chim bay thì người chiến sĩ phải bơi bao nhiêu mét để đến được mục tiêu nhanh nhất? (kết quả làm tròn đến hàng đơn vị)
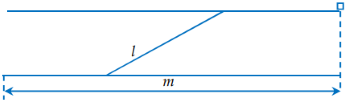
Trả lời:
Giám đốc một nhà hát A đang phân vân trong việc xác định mức giá vé xem các chương trình được trình chiếu trong nhà hát. Việc này rất quan trọng nó sẽ quyết định nhà hát thu được bao nhiêu lợi nhuận từ các buổi trình chiếu. Theo những cuốn sổ ghi chép của mình, ông ta xác định được rằng: nếu giá vé vào cửa là 20 USD/người thì trung bình có 1000 người đến xem. Nhưng nếu tăng thêm 1 USD/người thì sẽ mất 100 khách hàng hoặc giảm đi 1 USD/người thì sẽ có thêm 100 khách hàng trong số trung bình.Biết rằng, trung bình, mỗi khách hàng còn đem lại 2 USD lợi nhuận cho nhà hát trong các dịch vụ đi kèm. Giá vé vào cửa là bao nhiêu USD để thu nhập là lớn nhất?
Trả lời:

