Bài 36. Hình hộp chữ nhật và hình lập phương SVIP

1. Hình hộp chữ nhật, hình lập phương

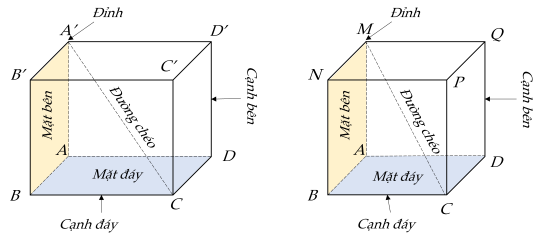
Hình hộp chữ nhật có 6 mặt là các hình chữ nhật, 8 đỉnh, 12 cạnh, 4 đường chéo, các cạnh bên song song và bằng nhau.

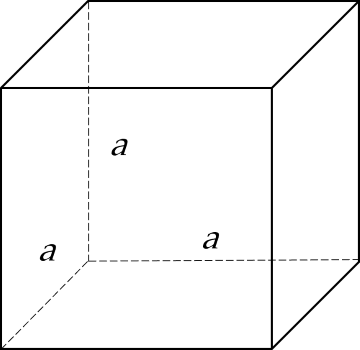
Hình lập phương là hình hộp chữ nhật có 6 mặt là các hình vuông.

 

2. Diện tích xung quanh và thể tích của hình hộp chữ nhật, hình lập phương

a.  Diện tích xung quanh của hình hộp chữ nhật, hình lập phương

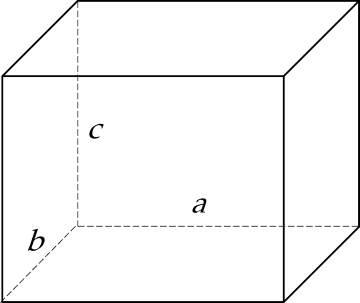
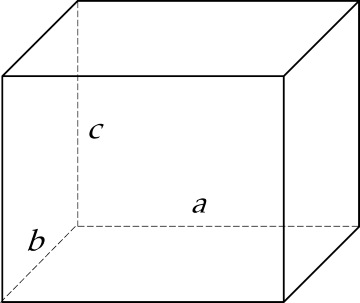
Diện tích xung quanh của hình hộp chữ nhật: $S_{xq} = 2(a+b)c$.

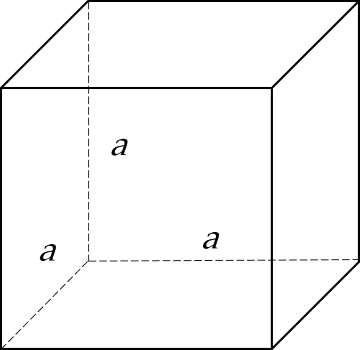
 Diện tích xung quanh của hình lập phương: $S_{xq} = 4a^2$.

 

Chú ý: Khi tính diện tích, thể tích của một hình, các kích thước của nó phải cùng đơn vị độ dài.

Ví dụ 1: Một chiếc khay nhựa đựng đồ có dạng hình hộp chữ nhật có chiều dài $27$ cm, chiều rộng $20$ cm, chiều cao $10$ cm. Ta coi mép khay nhựa không đáng kể, hãy tính:

a) Diện tích xung quanh của cái khay.

b) Diện tích nhựa để làm cái khay trên.

Giải

a) Diện tích xung quanh của chiếc khay dạng hình hộp chữ nhật là:

$2 \ .\ (27 + 20)\ .\ 10\ =\ 940$ (cm$^2$).

b) Diện tích nhựa để làm cái khay trên bằng tổng diện tích của các mặt xung quanh và mặt đáy.

Diện tích mặt đáy của chiếc khay là:

$27\ .\ 20\ =\ 540$ (cm$^2$).

Diện tích nhựa để làm chiếc khay là:

$940\ +\ 540\ =\ 1\ 480$ (cm$^2$).

b. Thể tích của hình hộp chữ nhật, hình lập phương

Thể tích hình hộp chữ nhật: $V\ =\ abc$.

Thể tích hình lập phương: $V\ =\ a^3$.

  

Ví dụ 2: Tính thể tích hộp sữa có dạng hình hộp chữ nhật có đáy là hình vuông cạnh $10$ cm, chiều cao $15$ cm.

Giải

Thể tích hộp sữ dạng hình hộp chữ nhật là:

$V\ =\ 10\ .\ 10.\ 15\ = 1\ 500$ (cm$^3$).