
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



+ Đạo hàm f'(x) = 1 - m ( x + 1 ) 2 .
+ Suy ra hàm số f(x) là hàm số đơn điệu trên đoạn [1; 2] với mọi m≠ 1.
+ Khi đó ta có :
m i n y [ 1 ; 2 ] + m a x [ 1 ; 2 ] y = f ( 1 ) + f ( 2 ) = m + 1 2 + m + 2 3 = 16 3 ↔ 5 m 6 = 25 6 ↔ m = 5
Chọn D.

+ Đạo hàm f'(x) = - m + 1 ( x - 1 ) 2
TH1. Với m> -1 suy ra f’(x) <0 mọi x≠ 1 nên hàm số f(x) nghịch biến trên mỗi khoảng xác định.
Khi đó m i n [ 2 ; 4 ] y = f ( 4 ) = m + 4 3 = 3 ↔ m = 5 (chọn).
TH2. Với m< -1 suy ra f”(x) > 0 mọi x≠1 nên hàm số f( x) đồng biến trên mỗi khoảng xác định.
Khi đó m i n [ 2 ; 4 ] y = f ( 2 ) = m + 2 = 3 ↔ m = 1 (loại).
Chọn C.

Chọn A
Ta có 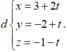 Vì M là giao điểmcủa d và (P) nên ta có tọa độ của M cũng thỏa mãn phương trình mặt phẳng (P) hay
Vì M là giao điểmcủa d và (P) nên ta có tọa độ của M cũng thỏa mãn phương trình mặt phẳng (P) hay

Gọi điểm H là hình chiếu của M lên
đường thẳng ∆ ta có
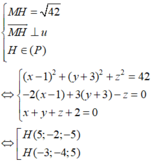
Vậy tồn tại hai đường thẳng ∆ thỏa mãn đề bài
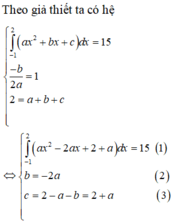
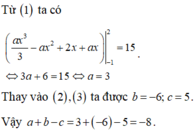
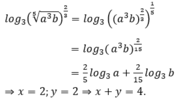

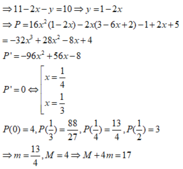



y + y + x = 2y + x.