
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đặt \(\dfrac{x}{y}+\dfrac{y}{x}=t\Rightarrow\left|t\right|\ge2\)
\(\dfrac{x^2}{y^2}+\dfrac{y^2}{x^2}=t^2-2\)
\(\dfrac{x^4}{y^4}+\dfrac{y^4}{x^4}=\left(\dfrac{x^2}{y^2}+\dfrac{y^2}{x^2}\right)^2-2=\left(t^2-2\right)^2-2=t^4-4t^2+2\)
\(\Rightarrow P=f\left(t\right)=t^4-4t^2+2-\left(t^2-2\right)+t\)
\(f\left(t\right)=t^4-5t^2+t+4\)
Xét hàm \(f\left(t\right)=t^4-5t^2+t+4\) trên \((-\infty;-2]\cup[2;+\infty)\)
\(f'\left(t\right)=g\left(t\right)=4t^3-10t+1\)
\(g\left(t\right)\) bậc 3 nên có tối đa 3 nghiệm
\(g\left(-2\right)=-11\) ; \(g\left(0\right)=1\)
\(\Rightarrow g\left(-2\right).g\left(0\right)< 0\Rightarrow g\left(t\right)=0\) có nghiệm \(t_1\in\left(-2;0\right)\)
\(g\left(1\right)=-5< 0\Rightarrow g\left(0\right).g\left(1\right)< 0\Rightarrow g\left(t\right)\) có nghiệm \(t_2\in\left(0;1\right)\)
\(g\left(2\right)=13\Rightarrow g\left(1\right).g\left(2\right)< 0\Rightarrow g\left(t\right)\) có nghiệm \(t_3\in\left(1;2\right)\)
Dấu \(f'\left(t\right)\):
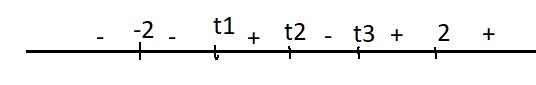
Từ đây ta thấy \(f\left(t\right)\) nghịch biến trên \((-\infty;-2]\) và đồng biến trên \([2;+\infty)\)
Hay GTNN của \(f\left(t\right)\) sẽ rơi vào \(t=-2\) hoặc \(t=2\)
\(f\left(-2\right)=-2\) ; \(f\left(2\right)=2\)
\(\Rightarrow f\left(t\right)_{min}=-2\) khi \(t=-2\) hay \(P_{min}=-2\) khi \(x=-y\)


a.
Pt giao điểm: \(cosx=0\Rightarrow x=\dfrac{\pi}{2}\)
\(S=\int\limits^{\pi}_0\left|cosx\right|dx=\int\limits^{\dfrac{\pi}{2}}_0cosxdx-\int\limits^{\pi}_{\dfrac{\pi}{2}}cosxdx=2\)
b.
Bạn coi lại đề, \(y=\dfrac{1}{2}x,x+\dfrac{1}{2}\) nghĩa là sao nhỉ?
c.
Pt giao điểm với Ox:
\(2-x-x^2=0\Rightarrow\left[{}\begin{matrix}x=1\\x=-2\end{matrix}\right.\)
\(S=\int\limits^1_{-2}\left(2-x-x^2\right)dx=\left(2x-\dfrac{1}{2}x^2-\dfrac{1}{3}x^3\right)|^1_{-2}=\dfrac{9}{2}\)

Xét trên các miền xác định của các hàm (bạn tự tìm miền xác định)
a.
\(y'=\dfrac{1}{2\sqrt{x-3}}-\dfrac{1}{2\sqrt{6-x}}=\dfrac{\sqrt{6-x}-\sqrt{x-3}}{2\sqrt{\left(x-3\right)\left(6-x\right)}}\)
\(y'=0\Rightarrow6-x=x-3\Rightarrow x=\dfrac{9}{2}\)
\(x=\dfrac{9}{2}\) là điểm cực đại của hàm số
b.
\(y'=1-\dfrac{9}{\left(x-2\right)^2}=0\Rightarrow\left(x-2\right)^2=9\Rightarrow\left[{}\begin{matrix}x=5\\x=-1\end{matrix}\right.\)
\(x=-1\) là điểm cực đại, \(x=5\) là điểm cực tiểu
c.
\(y'=\sqrt{3-x}-\dfrac{x}{2\sqrt{3-x}}=0\Rightarrow2\left(3-x\right)-x=0\)
\(\Rightarrow x=2\)
\(x=2\) là điểm cực đại
d.
\(y'=\dfrac{-x^2+4}{\left(x^2+4\right)^2}=0\Rightarrow\left[{}\begin{matrix}x=2\\x=-2\end{matrix}\right.\)
\(x=-2\) là điểm cực tiểu, \(x=2\) là điểm cực đại
e.
\(y'=\dfrac{-8\left(x^2-5x+4\right)}{\left(x^2-4\right)^2}=0\Rightarrow\left[{}\begin{matrix}x=1\\x=4\end{matrix}\right.\)
\(x=1\) là điểm cực tiểu, \(x=4\) là điểm cực đại

a) Đáp số: 1/6
b) Đáp số: 937/12.
Hướng dẫn:
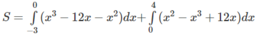
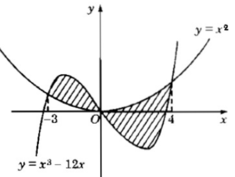
c) Đáp số: 2
Hướng dẫn: 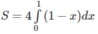
d) π/2 - 1
Hướng dẫn:
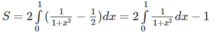
Đặt x = tan t để tính 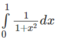
e) Đáp số: 27/4
Hướng dẫn: Phương trình tiếp tuyến tại (-1; -2) là y = 3x + 1. Do đó, diện tích :
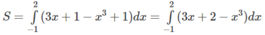
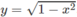 , y = 1 − x}
, y = 1 − x}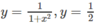
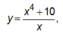
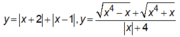
đây là toán lớp 12 ạ?!
Vui lòng không đăng lung tung lên diễn đàn nhé bạn.