K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
YD
2
VH
0
Dễ tek mà ko làm đc!
28 tháng 9 2017
Ta có: \(1^2+2^2+3^2+...+10^2=358\)
\(S=2^2+4^2+6^2+...+20^2\)
\(=\left(1.2\right)^2+\left(2.2\right)^2+\left(2.3\right)^2+...+\left(2.10\right)^2\)
\(=1^2.2^2+2^2.2^2+3^2.2^2+...+10^2.2^2\)
\(=2^2\left(1^2+2^2+3^2+...+10^3\right)\)
\(=2^2.385\)
\(=4.385=1540\)
MV
6 tháng 8 2017
Áp dụng tính chất dãy tỉ số bằng nhau ta có
\(\dfrac{x+y}{5}=\dfrac{x-y}{8}=\dfrac{x+y+x-y}{5+8}=\dfrac{2x}{13}=\dfrac{4x}{26}\)
Ta có:
\(\dfrac{x+y}{5}=\dfrac{xy}{26};\dfrac{x+y}{5}=\dfrac{4x}{26}\\ \Rightarrow\dfrac{xy}{26}=\dfrac{4x}{26}\Rightarrow y=4\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có
\(\dfrac{x+y}{5}=\dfrac{x-y}{8}=\dfrac{x+y-x+y}{5-8}=\dfrac{2y}{-3}\)
Ta có:
\(\dfrac{x-y}{8}=\dfrac{xy}{26};\dfrac{x-y}{8}=\dfrac{2y}{-3}\\ \Rightarrow\dfrac{xy}{26}=\dfrac{2y}{-3}\Rightarrow-3xy=52y\Leftrightarrow-3x=52\Rightarrow x=\dfrac{-52}{3}\)
Vậy \(x=-\dfrac{52}{3};y=4\)
19 tháng 8 2017
Ta có hình vẽ:
x x' O y y' \(\widehat{xOy}+\widehat{yOx'}+\widehat{x'Oy'}=297^o\)
\(\widehat{xOy}\) và \(\widehat{x'Oy'}\) đối đỉnh \(\Rightarrow\widehat{xOy}=\widehat{x'Oy'}\)
\(\widehat{x'Oy}\) và \(\widehat{x'Oy'}\) kề bù nên:
\(\widehat{x'Oy'}+\widehat{x'Oy}=180^o\)
\(\Rightarrow\widehat{xOy}+180^0=297^o\)
\(\Rightarrow\widehat{xOy}=117^o\)
\(\widehat{xOy}=\widehat{x'Oy'}=117^o\)
\(\Rightarrow\widehat{x'Oy}=297^o-117^o-177^o=3^o\)
\(\widehat{x'Oy}\) đối đỉnh với \(\widehat{xOy'}\) nên
\(\widehat{x'Oy}=\widehat{xOy'}=3^o\)
Vậy...
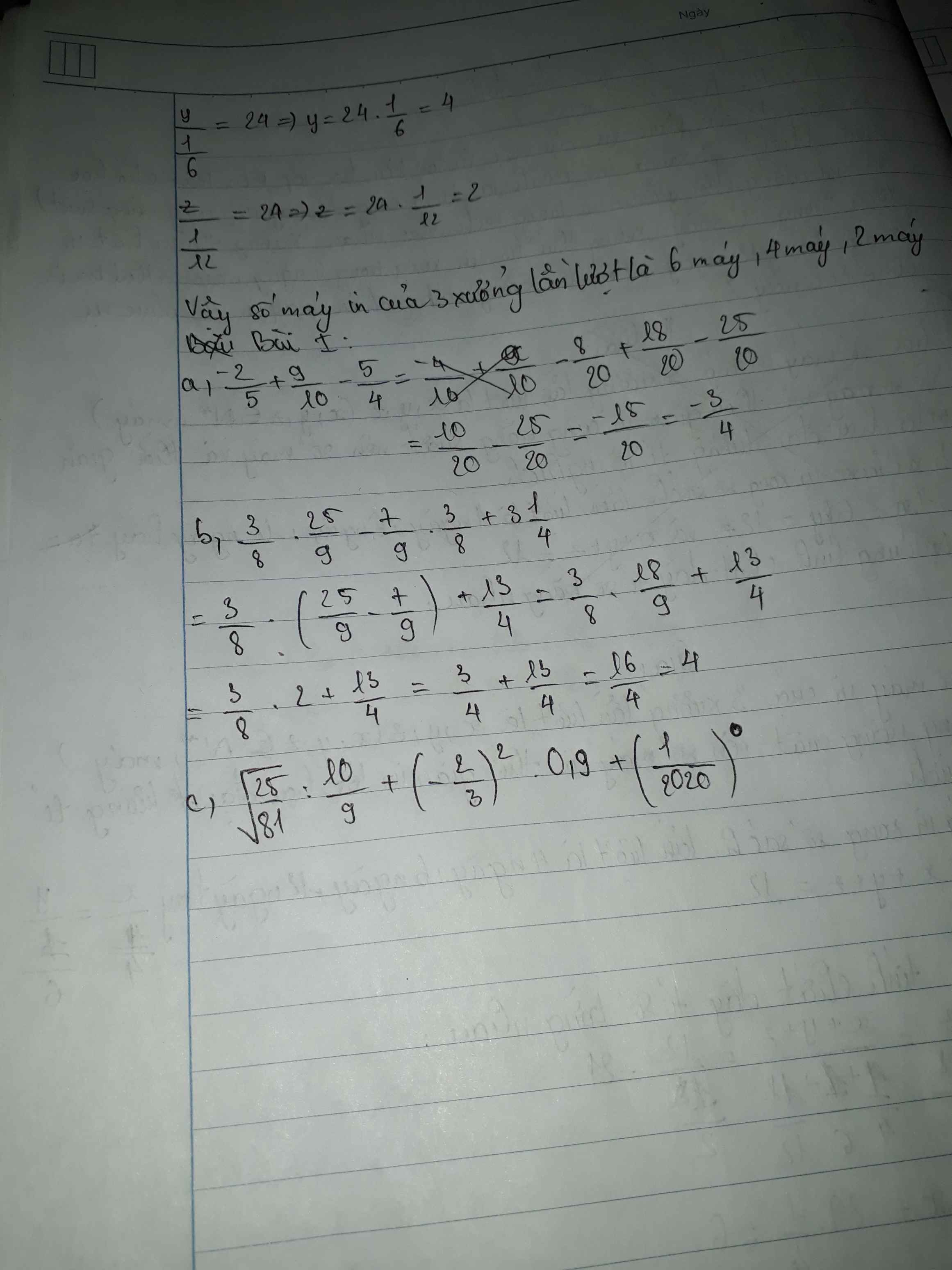
c: \(=\dfrac{5}{9}\cdot\dfrac{9}{10}+\dfrac{4}{9}\cdot\dfrac{9}{10}+1\)
\(=\dfrac{9}{10}+1=\dfrac{19}{10}\)
Thé 5/9 với 4/9