
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a,Ta có: x- 1/2= y- 2/3⇒ y= x- 1/2 +2/3= x+ 1/6
x- 1/2= z- 3/4⇒ z= x+ 1/4
⇒ x- 2y+3z= 24
⇔ x- 2( x+ 1/6)+ 3( x+1/4)= 24
⇔ x- 2x- 1/3+ 3x+ 3/4= 24
⇔ 2x= 283/12
⇔ x= 283/24
b, Ta có: xy= -30⇒ x= -30/y
yz= 42⇒ z= 42/y
lại có: z- x= -12
⇒ 42/y+ 30/y= -12
⇔ 72/y= -12
⇒ y= -6
⇒ x= 5; z= -7

(2): =>(4x^2-1)(x^2-6x+9)<=0
=>(4x^2-1)(x-3)^2<=0
TH1: (4x^2-1)(x-3)^2=0
=>x=3 hoặc \(x\in\left\{\dfrac{1}{2};-\dfrac{1}{2}\right\}\)
TH2: (4x^2-1)(x-3)^2<0
=>4x^2-1<0
=>-1/2<x<1/2

Hệ phương trình trở thành:
\(\hept{\begin{cases}\left(x+y\right)\left(x^2+y^2\right)=5\left(1\right)\\\left(x+y\right)\left(x-y\right)^2=3\left(2\right)\end{cases}}\)
Ta có: x+y khác 0; x-y khác 0
+) Với x =0 thay vào ta có hệ phương trình mới: \(\hept{\begin{cases}y.y^2=5\\y.y^2=3\end{cases}}\) loại
+) Với x khác 0, Đặt y=xt
Chia vế theo vế (1) cho (2), Ta có:
\(\frac{x^2+y^2}{\left(x-y\right)^2}=\frac{5}{3}\Leftrightarrow\frac{x^2+x^2t^2}{\left(x-xt\right)^2}=\frac{5}{3}\)
\(\Leftrightarrow\frac{1+t^2}{\left(1-t\right)^2}=\frac{5}{3}\)
\(\Leftrightarrow3\left(1+t^2\right)=5\left(1-t\right)^2\)
\(\Leftrightarrow2t^2-10t+2=0\Leftrightarrow\orbr{\begin{cases}t=\frac{5+\sqrt{21}}{2}\\t=\frac{5-\sqrt{21}}{2}\end{cases}}\)
Ta có: y=xt thế vào phương trình (1) hoặc (2) ta có phương trình ẩn x. Gợi ý như vậy em làm tiếp nhé! :)

Bài này trước giải bằng lượng giác chắc bạn Nguyệt Hà chưa hiểu, giờ mình giải bằng Đại số nhé!
Phương trình tương đương với
\(x-\sqrt{1-x^2}=\sqrt{2}x.\sqrt{1-x}\)
Đặt \(t=x-\sqrt{1-x^2}\) thì \(x\sqrt{1-x^2}=\dfrac{1-t^2}{2}\). Phương trình trở thành \(t=\sqrt{2}.\dfrac{1-t^2}{2}\).
Tìm được t sẽ suy ra x nhé!

1.A. Ta thấy để hàm số xác định thì x-m\(\ne\)0 hay x\(\ne\)m mà vì x\(\in\)(0,1) nên để x\(\ne\)m thì m\(\notin\)(0,1)=>m>=1 hoặc m<=0
2A để A giao B khác 0 thì 2m-1<=m+3 hay m<=4
3C.A giao B =A khi \(\left\{{}\begin{matrix}m< =-1\\m+5>=3\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}m< =1\\m>=-2\end{matrix}\right.\)

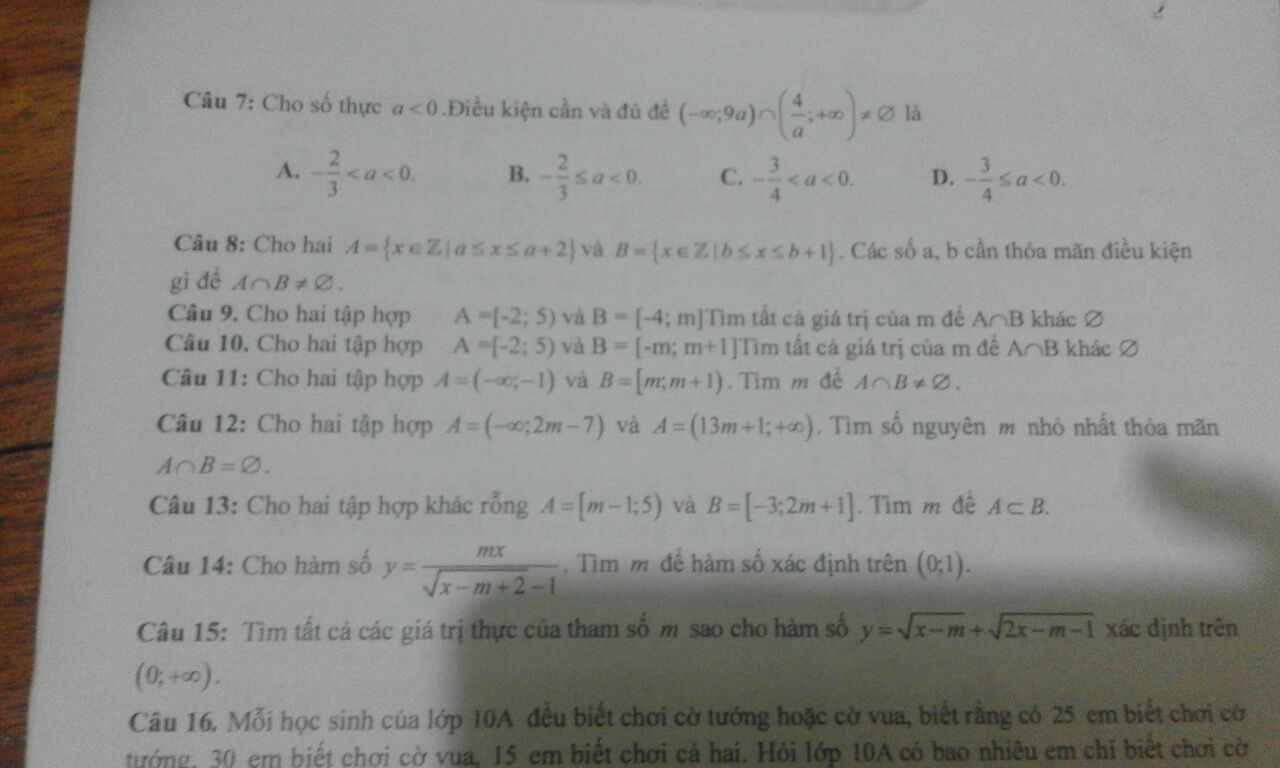 GIÚP MK VS!!! MAI MK PHẢI NỘP RỒI!!!!!!!!
GIÚP MK VS!!! MAI MK PHẢI NỘP RỒI!!!!!!!!
\(xy-x+y-1=-1\Leftrightarrow\left(x+1\right)\left(y-1\right)=-1\)
\(\Rightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x+1=1\\y-1=-1\end{matrix}\right.\\\left\{{}\begin{matrix}x+1=-1\\y-1=1\end{matrix}\right.\end{matrix}\right.\) ......
mk nhầm toán 10 nhé
sorry