K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
23 tháng 9 2021
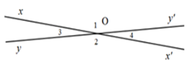
\(a,\widehat{x'Oy'}=\widehat{xOy}=70^0\left(2.góc.đđ\right)\)
\(b,\widehat{x'Oy}.đối.đỉnh.\widehat{xOy'}\) do \(Ox.đối.Ox';Oy.đối.Oy'\)
\(c,\widehat{xOy'}+\widehat{xOy}=180^0\left(kề.bù\right)\\ \Rightarrow\widehat{xOy'}=180^0-70^0=110^0\\ \widehat{xOy'}=\widehat{x'Oy}=110^0\left(đối.đỉnh\right)\)
10 tháng 9 2020
Mình ko biết đăng hình nên bn tự lên mạng tra nhé :
Đây là 6 cặp góc đối đỉnh !
xOyˆ đối đỉnh x′Oy′ˆ
xOtˆ đối đỉnh x′Ot′ˆ
yOtˆ đối đỉnh y′Ot′ˆ
xOy′ˆ đối đỉnh x′Oyˆ
x′Otˆ đối đỉnh xOt′ˆ
yOt′ˆ đối đỉnh y′Otˆ
10 tháng 9 2020
6 cặp góc đối đỉnh :
xOtˆ đối đỉnh với x′Ot′ˆ => xOtˆ=x′Ot′ˆ (1)
tOyˆ đối đỉnh với t′Oy′ˆ => tOyˆ=t′Oy′ˆ (2)
xOyˆ đối đỉnh với x′Oy′ˆ => xOyˆ=x′Oy′ˆ (3)
Ta có: xOyˆ=60 độ =>(3) xOyˆ=x′Oy′ˆ=60 độ
Vì Ot là tia phân giác của góc xOy
=> xOtˆ=tOyˆ=602=30độ
Từ (1),(2) => tOyˆ=t′Oy′ˆ=xOyˆ=x′Oy′ˆ=30độ
Q
8 tháng 9 2017
+ Ta có góc xÔy đối đỉnh với góc x'Ôy'
=> Ox là tia đối của tia Oy'
=> xÔy' = 180o
Ta có góc xÔy đối đỉnh với góc x'Ôy'
=> Oy là tia đối của tia Ox'
=> x'Ôy = 180o
Vì góc xÔy đối đỉnh x'Ôy' nên :
xÔy = x'Ôy' = 75o
Vậy x'Ôy' = 75o
+ Vì xÔy là góc đổi đỉnh x'Ôy' mà Ot và Ot' lần lượt là tia phân giác của xÔy và x'Ôy'
Nên => xÔy/2 = x'Ôy'/2 (1)
=> xÔt = tÔy = xÔy/2 (2)
=> x'Ôt' = t'Ôy' = x'Ôy'/2 (3)
Từ (1),(2) và (3) => xÔt = x'Ôt' (*)
=> tÔy = t'Ôy' (**)
Từ (*) và (**) => đpcm
