Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta sẽ chứng minh \(\left(u_n\right)\) giảm, tức \(u_{n+1}< u_n\) (*) bằng phương pháp quy nạp.
Với n = 1: \(u_2-u_1=\dfrac{u_1^2+1}{4}-u_1=\dfrac{2^2+1}{4}-2=\dfrac{-3}{4}< 0\)
Giả sử (*) đúng với n = k (\(k\in N;k>1\)), tức \(u_{k+1}< u_k\)
Ta sẽ chứng minh (*) đúng với n = k + 1, tức \(u_{k+2}< u_{k+1}\)
\(u_{k+2}=\dfrac{\left(u_{k+1}\right)^2+1}{4}< \dfrac{u_k^2+1}{4}=u_{k+1}\)
Theo nguyên lí quy nạp, ta được đpcm.
Vậy \(\left(u_n\right)\) giảm.

1:
a: \(u_2=2\cdot1+3=5;u_3=2\cdot5+3=13;u_4=2\cdot13+3=29;\)
\(u_5=2\cdot29+3=61\)
b: \(u_2=u_1+2^2\)
\(u_3=u_2+2^3\)
\(u_4=u_3+2^4\)
\(u_5=u_4+2^5\)
Do đó: \(u_n=u_{n-1}+2^n\)

Bạn tham khảo câu trả lời của anh Lâm
https://hoc24.vn/cau-hoi/.334447965337

a)
\(u_1=5\)
\(u_2-u_1=1\)
\(u_3-u_2=4\)
............
\(u_n-u_{n-1}=3\left(n-1\right)-2=3n-5\)
Cộng từng vế của đẳng thức và rút gọn ta được:
\(u_n=5+1+4+7+...+3n-5\)
\(=5+\dfrac{\left(3n-5+1\right)\left(n-1\right)}{2}=5+\dfrac{\left(3n-4\right)\left(n-1\right)}{2}\).
Vậy \(u_n=5+\dfrac{\left(3n-4\right)\left(n-1\right)}{2}\) với \(n\ge1\).
Xét hiệu:
\(u_1=5\)
\(u_n-u_{n-1}=3n-5\) \(\left(n\ge2\right)\)
Với \(n\ge2\) thì \(3n-5>0\) nên \(u_n>u_{n-1}\).
Vậy \(\left(u_n\right)\) là dãy số tăng.




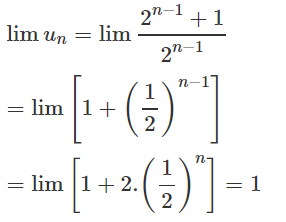
Trước hết ta chứng minh \(0< u_n\le1+\sqrt{2}\):
Ta thấy: \(0< u_1=2\le1+\sqrt{2}\)
Giả sử điều này đúng đến \(0< u_k\le1+\sqrt{2}\)
Ta có: \(u_{k+1}=\dfrac{3u_k+1}{u_k+1}>0\)
Lại có: \(u_{k+1}=\dfrac{3u_k+1}{u_k+1}=3-\dfrac{2}{u_k+1}\le3-\dfrac{2}{1+\sqrt{2}}\le3-1=2\le1+\sqrt{2}\)
\(\Rightarrow0< u_{k+1}\le1+\sqrt{2}\)
Theo nguyên lí quy nạp, ta được: \(0< u_n\le1+\sqrt{2}\)
Khi đó ta có:
\(u_{n+1}-u_n=\dfrac{3u_n+1}{u_n+1}-u_{n\text{}}\)
\(=\dfrac{3u_n+1-u_n^2-u_n}{u_n+1}\)
\(=\dfrac{-u_n^2+2u_n+1}{u_n+1}\)
\(=-\dfrac{\left(u_n-1-\sqrt{2}\right)\left(u_n-1+\sqrt{2}\right)}{u_n+1}\ge0\)
\(\Rightarrow u_{n+1}\ge u_n\)
\(\Rightarrow\) Dãy tăng.