Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
Có:
\(u_{n+1}-u_n=\sqrt{n+4}-\sqrt{n+1}-(\sqrt{n+3}-\sqrt{n})\)
\(=(\sqrt{n+4}-\sqrt{n+3})-(\sqrt{n+1}-\sqrt{n})\)
\(=\frac{1}{\sqrt{n+4}+\sqrt{n+3}}-\frac{1}{\sqrt{n+1}+\sqrt{n}}<0\) với mọi $n\in\mathbb{N}^*$
$\Rightarrow u_{n+1}< u_n$ với mọi $n\in\mathbb{N}^*$
Do đó dãy đã cho là dãy giảm.

Lời giải:
Thấy rằng $u_n>0$ với mọi $n\in\mathbb{N}^*$
\(\frac{u_{n+1}}{u_n}=\frac{\sqrt{n+12}}{n+1}: \frac{\sqrt{n+11}}{n}=\frac{\sqrt{n^2(n+12)}}{\sqrt{(n+1)^2(n+11)}}=\sqrt{\frac{n^3+12n^2}{n^3+13n^2+23n+11}}<1\) với mọi $n\in\mathbb{N}^*$
$\Rightarrow u_{n+1}< u_n$ với mọi $n\in\mathbb{N}^*$
$\Rightarrow (u_n)$ là dãy giảm.

Dãy đã cho hiển nhiên là dãy dương
Ta sẽ chứng minh dãy đã cho bị chặn trên bởi 2 hay \(u_n\le2\) với mọi n
- Với \(n=1\Rightarrow u_1=\sqrt{2}< 2\) (đúng)
- Giả sử điều đó đúng với \(n=k\ge1\) hay \(u_k\le2\)
- Ta cần chứng minh với \(n=k+1\) cũng đúng
Hay \(u_{k+1}\le2\)
Ta có: \(u_{k+1}=\sqrt{2+u_k}\le\sqrt{2+2}=2\) (đpcm)
Vậy \(u_n\le2\)
Đặt \(v_n=\dfrac{1}{2}u_n\Rightarrow0< v_n\le1\) và \(\left\{{}\begin{matrix}v_1=\dfrac{\sqrt{2}}{2}=cos\left(\dfrac{\pi}{4}\right)\\2v_{n+1}=\sqrt{2+2v_n}\end{matrix}\right.\)
\(\Rightarrow4v_{n+1}^2=2+2v_n\Rightarrow v_n=2v_{n+1}^2-1\)
Do \(0< v_n\le1\) , đặt \(v_n=cos\left(x_n\right)\) với \(x_n\in\left(0;\pi\right)\)
\(\Rightarrow\left\{{}\begin{matrix}x_1=\dfrac{\pi}{4}\\cos\left(x_n\right)=2cos^2\left(x_{n+1}\right)-1=cos\left(2x_{n+1}\right)\end{matrix}\right.\)
\(\Rightarrow x_n=2x_{n+1}\Rightarrow x_{n+1}=\dfrac{1}{2}x_n\)
\(\Rightarrow x_n\) là CSN với công bội \(\dfrac{1}{2}\)
\(\Rightarrow x_n=\dfrac{\pi}{4}.\left(\dfrac{1}{2}\right)^{n-1}=\dfrac{\pi}{2^{n+1}}\)
\(\Rightarrow v_n=cos\left(x_n\right)=cos\left(\dfrac{\pi}{2^{n+1}}\right)\)
\(\Rightarrow u_n=2v_n=2cos\left(\dfrac{\pi}{2^{n+1}}\right)\)
Dãy \(\dfrac{\pi}{2^{n+1}}\) giảm và thuộc \(\left(0;\dfrac{\pi}{2}\right)\) nên \(cos\left(\dfrac{\pi}{2^{n+1}}\right)\) tăng
Do đó dãy số đã cho là dãy tăng.
P/s: đây là cách làm hoàn chỉnh có thứ tự (nhược điểm là rất dài). Có 1 cách khác đơn giản hơn là bằng 1 phép màu nào đó ngay từ đầu bạn đưa ra ngay dự đoán công thức tổng quát của dãy số là \(2cos\left(\dfrac{\pi}{2^{n+1}}\right)\) rồi chứng minh nó bằng quy nạp cũng được. Như vậy sẽ rất ngắn, cả bài chỉ 4-5 dòng nhưng lời giải hơi đột ngột

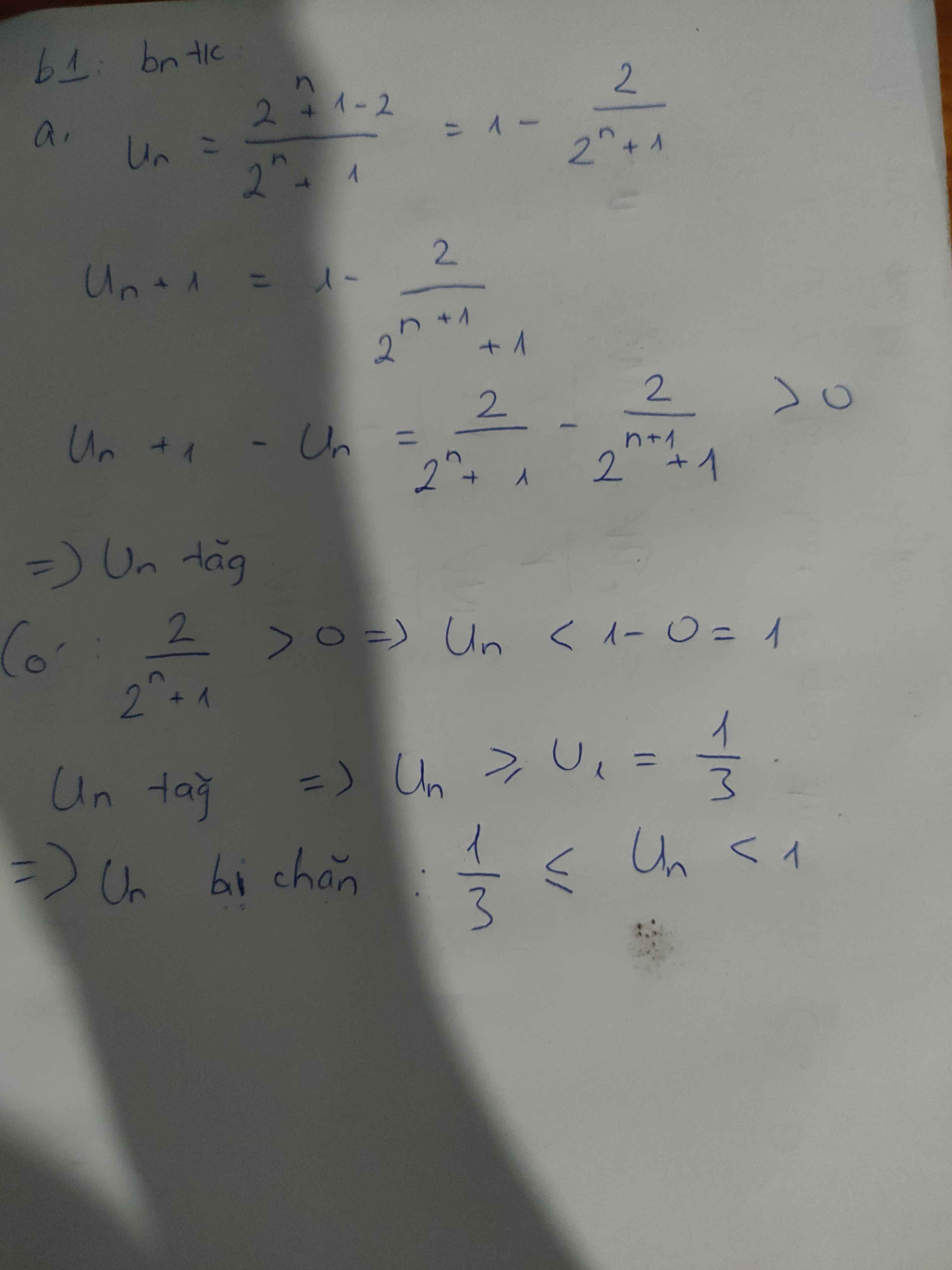
Cách 1:
Ta có: \({y_n} = \sqrt {n + 1} - \sqrt n = \frac{{\left( {\sqrt {n + 1} - \sqrt n } \right)\left( {\sqrt {n + 1} + \sqrt n } \right)}}{{\sqrt {n + 1} + \sqrt n }} = \frac{{\left( {n + 1} \right) - n}}{{\sqrt {n + 1} + \sqrt n }} = \frac{1}{{\sqrt {n + 1} + \sqrt n }}\)
\( \Rightarrow {y_{n + 1}} = \frac{1}{{\sqrt {\left( {n + 1} \right) + 1} - \sqrt {n + 1} }} = \frac{1}{{\sqrt {n + 2} + \sqrt {n + 1} }}\)
Xét hiệu:
\(\begin{array}{l}{y_{n + 1}} - {y_n} = \frac{1}{{\sqrt {n + 2} + \sqrt {n + 1} }} - \frac{1}{{\sqrt {n + 1} + \sqrt n }} = \frac{{\left( {\sqrt {n + 1} + \sqrt n } \right) - \left( {\sqrt {n + 2} + \sqrt {n + 1} } \right)}}{{\left( {\sqrt {n + 2} + \sqrt {n + 1} } \right)\left( {\sqrt {n + 1} + \sqrt n } \right)}}\\ = \frac{{\sqrt {n + 1} + \sqrt n - \sqrt {n + 2} - \sqrt {n + 1} }}{{\left( {\sqrt {n + 2} + \sqrt {n + 1} } \right)\left( {\sqrt {n + 1} + \sqrt n } \right)}} = \frac{{\sqrt n - \sqrt {n + 2} }}{{\left( {\sqrt {n + 2} + \sqrt {n + 1} } \right)\left( {\sqrt {n + 1} + \sqrt n } \right)}}\end{array}\)
\(\forall n \in {\mathbb{N}^*}\) ta có:
\(\begin{array}{l}\left. \begin{array}{l}0 < n < n + 2 \Leftrightarrow \sqrt n < \sqrt {n + 2} \Leftrightarrow \sqrt n - \sqrt {n + 2} < 0\\\sqrt {n + 2} > 0,\sqrt {n + 1} > 0,\sqrt n > 0 \Leftrightarrow \left( {\sqrt {n + 2} + \sqrt {n + 1} } \right)\left( {\sqrt {n + 1} + \sqrt n } \right) > 0\end{array} \right\}\\ \Rightarrow \frac{{\sqrt n - \sqrt {n + 2} }}{{\left( {\sqrt {n + 2} + \sqrt {n + 1} } \right)\left( {\sqrt {n + 1} + \sqrt n } \right)}} < 0\end{array}\)
Vậy \({y_{n + 1}} - {y_n} < 0 \Leftrightarrow {y_{n + 1}} < {y_n}\). Vậy dãy số \(\left( {{y_n}} \right)\) là dãy số giảm.
Cách 2:
Ta có: \({y_n} = \sqrt {n + 1} - \sqrt n = \frac{{\left( {\sqrt {n + 1} - \sqrt n } \right)\left( {\sqrt {n + 1} + \sqrt n } \right)}}{{\sqrt {n + 1} + \sqrt n }} = \frac{{\left( {n + 1} \right) - n}}{{\sqrt {n + 1} + \sqrt n }} = \frac{1}{{\sqrt {n + 1} + \sqrt n }}\)
\( \Rightarrow {y_{n + 1}} = \frac{1}{{\sqrt {\left( {n + 1} \right) + 1} - \sqrt {n + 1} }} = \frac{1}{{\sqrt {n + 2} + \sqrt {n + 1} }}\)
\(\forall n \in {\mathbb{N}^*}\) ta có:
\(\begin{array}{l}0 < n < n + 2 \Leftrightarrow \sqrt n < \sqrt {n + 2} \Leftrightarrow \sqrt {n + 1} + \sqrt n < \sqrt {n + 2} + \sqrt {n + 1} \\ \Leftrightarrow \frac{1}{{\sqrt {n + 1} + \sqrt n }} > \frac{1}{{\sqrt {n + 2} + \sqrt {n + 1} }} \Leftrightarrow {y_n} > {y_{n + 1}}\end{array}\)
Vậy dãy số \(\left( {{y_n}} \right)\) là dãy số giảm.