
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn D.
Ta có:
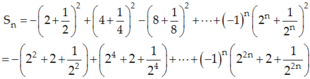
![]()

- Có dãy số -22, 24, …, (-1)n.22n là cấp số nhân với n số hạng, có số hạng đầu u1 = -4 và công bội q = -4.
Do đó 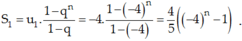
- Có dãy số  là cấp số nhân với n số hạng, có số hạng đầu
là cấp số nhân với n số hạng, có số hạng đầu 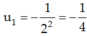 và công bội q = -1/4.
và công bội q = -1/4.
Do đó 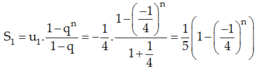
Vậy 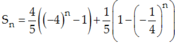


1/ \(\lim\limits_{x\rightarrow2^+}f\left(x\right)=\lim\limits_{x\rightarrow2^+}\left(x+1\right)=f\left(2\right)=3\)
\(\lim\limits_{x\rightarrow2^-}f\left(x\right)=\lim\limits_{x\rightarrow2^-}\dfrac{\left(x-2\right)\left(x-1\right)}{\left(x-2\right)\left(x^2+2x+4\right)}=\lim\limits_{x\rightarrow2^-}\dfrac{x-1}{x^2+2x+4}=\dfrac{1}{12}\)
\(\lim\limits_{x\rightarrow2^+}f\left(x\right)=f\left(2\right)\ne\lim\limits_{x\rightarrow2^-}f\left(x\right)\)
=> ham so gian doan tai x=2
2/ \(\lim\limits_{x\rightarrow2^-}f\left(x\right)=f\left(2\right)=2a-1\)
\(\lim\limits_{x\rightarrow2^+}f\left(x\right)=\lim\limits_{x\rightarrow2^+}\dfrac{3x-2-4}{\left(x-2\right)\left(\sqrt{3x-2}+2\right)}=\lim\limits_{x\rightarrow2^+}\dfrac{3}{\sqrt{3x-2}+2}=\dfrac{3}{4}\)
De ham so lien tuc tai x=2
\(\Leftrightarrow\lim\limits_{x\rightarrow2^-}f\left(x\right)=f\left(2\right)=\lim\limits_{x\rightarrow2^+}f\left(x\right)\Leftrightarrow2a-1=\dfrac{3}{4}\Leftrightarrow a=\dfrac{7}{8}\)

a) Dãy số un = 2n - 1: Đây là một dãy số tăng với hệ số tăng là 2.
b) Dãy số un = 3 - 2n: Đây là một dãy số giảm với hệ số giảm là 2.
c) Dãy số un = n + 2n: Đây là một dãy số tăng với hệ số tăng là 3.
d) Dãy số un = 2n: Đây là một dãy số tăng với hệ số tăng là 2.
e) Dãy số un = 3n: Đây là một dãy số tăng với hệ số tăng là 3.
a: \(u_{n+1}-u_n=2\left(n+1\right)-1-2n+1\)
\(=2n+2-2n=2>0\)
=>Đây là dãy tăng
b: \(u_{n+1}-u_n=-2\left(n+1\right)+3+2n-3=-2n-2+2n=-2< 0\)
=>Đây là dãy giảm
d: \(u_{n+1}-u_n=\dfrac{2}{n+1}-\dfrac{2}{n}=\dfrac{2n-2n-2}{n\left(n+1\right)}=-\dfrac{2}{n\left(n+1\right)}< 0\)
=>Đây là dãy giảm
e: \(\dfrac{u_{n+1}}{u_n}=\dfrac{3^{n+1}}{3^n}=3>1\)
=>Đây là dãy tăng


Ta có:
\(n^5+n^4-2n^3-2n^2+1=p^k\Leftrightarrow\left(n^2+n-1\right)\left(n^3-n-1\right)=p^k\)
Từ gt \(\Rightarrow n,k\ge2\)
Ta có:
\(\left\{{}\begin{matrix}n^3-n-1>1;n^2+n-1>1,\forall n\ge2\\\left(n^3-n-1\right)-\left(n^2+n-1\right)=\left(n+1\right)n\left(n-2\right)\ge0,\forall n\ge2\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}n^3-n-1=p^r\\n^2+n-1=p^s\end{matrix}\right.\) trong đó \(\left\{{}\begin{matrix}r\ge s>0\\r+s=k\end{matrix}\right.\)
\(\Rightarrow n^3-n-1⋮n^2+n-1\)
\(\Rightarrow n^3-n-1-\left(n-1\right)\left(n^2+n-1\right)⋮n^2+n-1\)
\(\Rightarrow n-2⋮n^2+n-1\) (1)
Mặt khác:
\(\left(n^2+n-1\right)-\left(n-2\right)=n^2+1>0,\forall n\)
\(\Rightarrow n^2+n-1>n-2\ge0,\forall n\ge2\) (2)
Từ (1) và (2) => n=2 => \(p^k=25\Rightarrow\left\{{}\begin{matrix}p=5\\k=2\end{matrix}\right.\)
Vậy bộ số (n,k,p)=(2,2,5)
\(...\Leftrightarrow\left(n^2+n-1\right)\left(n^3-n-1\right)=p^k\).
Do đó \(\left\{{}\begin{matrix}n^2+n-1=p^v\\n^3-n-1=p^u\end{matrix}\right.\left(v,u\in N;v+u=k\right)\).
+) Với n = 2 ta có \(p^k=25=5^2\Leftrightarrow p=5;k=2\)
+) Với n > 2 ta có \(n^3-n-1>n^2+n-1\Rightarrow v>u\Rightarrow n^3-n-1⋮n^2+n-1\)
\(\Rightarrow\left(n^2+n-1\right)\left(n-1\right)+n-2⋮n^2+n-1\)
\(\Rightarrow n-2⋮n^2+n-1\)
\(\Rightarrow\left(n-2\right)\left(n+3\right)⋮n^2+n-1\)
\(\Rightarrow6⋮n^2+n-1\).
Không tồn tại n > 2 thoả mãn
Vậy...

• Ta có: \({u_{n + 1}} = \frac{{2\left( {n + 1} \right) - 1}}{{\left( {n + 1} \right) + 1}} = \frac{{2n + 2 - 1}}{{n + 1 + 1}} = \frac{{2n + 1}}{{n + 2}}\)
Xét hiệu:
\(\begin{array}{l}{u_{n + 1}} - {u_n} = \frac{{2n + 1}}{{n + 2}} - \frac{{2n - 1}}{{n + 1}} = \frac{{\left( {2n + 1} \right)\left( {n + 1} \right) - \left( {2n - 1} \right)\left( {n + 2} \right)}}{{\left( {n + 2} \right)\left( {n + 1} \right)}}\\ = \frac{{\left( {2{n^2} + n + 2n + 1} \right) - \left( {2{n^2} - n + 4n - 2} \right)}}{{\left( {n + 2} \right)\left( {n + 1} \right)}}\\ = \frac{{2{n^2} + n + 2n + 1 - 2{n^2} + n - 4n + 2}}{{\left( {n + 2} \right)\left( {n + 1} \right)}} = \frac{3}{{\left( {n + 2} \right)\left( {n + 1} \right)}} > 0,\forall n \in {\mathbb{N}^*}\end{array}\)
Vậy \({u_{n + 1}} - {u_n} > 0 \Leftrightarrow {u_{n + 1}} > {u_n}\). Vậy dãy số \(\left( {{u_n}} \right)\) là dãy số tăng.
• Ta có: \({u_n} = \frac{{2n - 1}}{{n + 1}} = \frac{{2\left( {n + 1} \right) - 3}}{{n + 1}} = 2 - \frac{3}{{n + 1}}\)
\(\forall n \in {\mathbb{N}^*}\) ta có:
\(n + 1 > 0 \Leftrightarrow \frac{3}{{n + 1}} > 0 \Leftrightarrow 2 - \frac{3}{{n + 1}} < 2 \Leftrightarrow {u_n} < 2\). Vậy \(\left( {{u_n}} \right)\) bị chặn trên.
\(n \ge 1 \Leftrightarrow n + 1 \ge 1 + 1 \Leftrightarrow n + 1 \ge 2 \Leftrightarrow \frac{3}{{n + 1}} \le \frac{3}{2} \Leftrightarrow 2 - \frac{3}{{n + 1}} \ge 2 - \frac{3}{2} \Leftrightarrow {u_n} \ge \frac{1}{2}\)
Vậy \(\left( {{u_n}} \right)\) bị chặn dưới.
Ta thấy dãy số \(\left( {{u_n}} \right)\) bị chặn trên và bị chặn dưới nên dãy số \(\left( {{u_n}} \right)\) bị chặn.

a) Ta có: \({u_{n + 1}} - {u_n} =[2\left( {n + 1} \right) - 1] - (2n - 1) = 2\left( {n + 1} \right) - 1 - 2n + 1 = 2 > 0 \Rightarrow {u_{n + 1}} > {u_n},\;\forall \;n \in {N^*}\)
Vậy \(\left( {{u_n}} \right)\) là dãy số tăng.
b) Ta có: \({u_{n + 1}} - {u_n} = [- 3\left( {n + 1} \right) + 2] - (3n + 2) = - 3\left( {n + 1} \right) + 2 + 3n - 2 = - 3 < 0\;\)
Vậy \(\left( {{u_n}} \right)\) là dãy số giảm.
c, Ta có:
\(\begin{array}{l}{u_1} = \frac{{{{( - 1)}^{1 - 1}}}}{{{2^1}}} = \frac{1}{2} > 0\\{u_2} = \frac{{{{( - 1)}^{2 - 1}}}}{{{2^2}}} = - \frac{1}{4} < 0\\{u_3} = \frac{{{{( - 1)}^{3 - 1}}}}{{{2^3}}} = \frac{1}{8} > 0\\{u_4} = \frac{{{{( - 1)}^{4 - 1}}}}{{{2^4}}} = - \frac{1}{{16}} < 0\\...\end{array}\)
Vậy \(\left( {{u_n}} \right)\) là dãy số không tăng không giảm.

Ta có:
\(n^5+n^4-2n^3-2n^2+1=p^k\Leftrightarrow\left(n^2+n-1\right)\left(n^3-n-1\right)=p^k\)
Từ giả thiết \(\Rightarrow n,k\ge2\)
Ta có:
\(\hept{\begin{cases}n^3-n-1>1,n^2+n-1>1,\forall n\ge2\\\left(n^3-n-1\right)-\left(n^2+n-1\right)=\left(n+1\right)n\left(n-2\right)\ge0,\forall n\ge2\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}n^3-n-1=p^r\\n^2+n-1=p^s\end{cases}}\) trong đó \(\hept{\begin{cases}r\ge s\ge0\\r+s=k\end{cases}}\)
\(\Rightarrow n^3-n-1⋮n^2+n-1\)
\(\Rightarrow n^3-n-1-\left(n-1\right)\left(n^2+n-1\right)⋮n^2+n-1\)
\(\Rightarrow n-2⋮n^2+n-1\) (1)
Mặt khác :
\(\left(n^2+n-1\right)-\left(n-2\right)=n^2+1>0,\forall n\)
\(\Rightarrow n^2+n-1>n-2\ge0,\forall n\ge2\) (2)
Từ (1) và (2) => n=2 => \(p^k=25\Rightarrow\hept{\begin{cases}p=5\\k=2\end{cases}}\)
Vậy bộ số cần tìm là (n,k,p)=(2,2,5)
A=\(u_{n+1}-u_n=\left(2n+2-5\right)\cdot\left(-1\right)^{n+1}-\left(2n-5\right)\cdot\left(-1\right)^n\)
\(=\left(2n-3\right)\cdot\left(-1\right)^{n+1}-\left(2n-5\right)\cdot\left(-1\right)^n\)
TH1:n là số chẵn
=>A=-(2n-3)-(2n-5)=-2n+3-2n+5=-4n+8
\(u_{n+1}-u_n=-4\left(n+1\right)+8+4n-8=-4n-4+4n=-4< 0\)
=>Dãy số giảm
TH2: n là số lẻ
A=(2n-3)-(2n-5)*(-1)
=2n-3+2n-5=4n-8
\(u_{n+1}-u_n=4\left(n+1\right)-8-4n+8=4>0\)
=>Dãy số tăng