LM
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
8 tháng 9 2021
Trên \(\left(-\dfrac{\pi}{2}+k.2\pi;\dfrac{\pi}{2}+k.2\pi\right)\) chọn 2 giá trị của x (x1 và x2) sao cho x1 > x2
Xét f(x1) - f(x2) = sinx1 - sinx2
= 2cos\(\dfrac{x_1+x_2}{2}\) . sin \(\dfrac{x_1-x_2}{2}\)
Do \(\dfrac{x_1+x_2}{2}\in\left(0;\dfrac{\pi}{2}\right)\)
⇒ cos\(\dfrac{x_1+x_2}{2}\) > 0
Mà \(sin\dfrac{x_1-x_2}{2}\) > 0
nên f(x1) - f(x2) > 0
Vậy đồng biến
Nghịch biến tương tự
8 tháng 9 2021
tại sao \(\dfrac{x_1+x_2}{2}\in\left(0;\dfrac{\pi}{2}\right)\)ạ ?
K
5 tháng 8 2020
Ta có \(y'=x^2-x\left(sina+cosa\right)+\frac{3}{4}sin2a\)
Để y có cực đại và cực tiểu thì y' đổi dấu hai lần, tức là:
\(\Delta=\left(sina+cosa\right)^2-3sin2a>0\)
\(\Leftrightarrow1+sin2a-3sin2a>0\)
\(\Leftrightarrow sin2a< \frac{1}{2}\)
\(\Leftrightarrow\frac{5\eta}{6}+k2\eta< 2a< \frac{13\eta}{6}+k2\eta\)
\(\Leftrightarrow\frac{5\eta}{12}+k\eta< a< \frac{13\eta}{12}+k\eta\)
K
5 tháng 8 2020
Tại cực trị \(y'=0\Leftrightarrow x^2-x\left(sina+cosa\right)+\frac{3}{4}sin2a=0\)(*)
(*) cho ta\(x_1+x_2=sina+cosa,x_1x_2=\frac{3}{4}sin2a\)(*)
Để \(x_1+x_2=x^2_1+x^2_2\)thì \(x_1+x_2=\left(x_1+x_2\right)^2-2x_1+x_2\)
\(\Leftrightarrow sina+cosa=\left(sina+cosa\right)^2-\frac{3}{2}sin2a\)
\(\Leftrightarrow sina+cosa=1-\frac{1}{2}sin2a\)
Đặt \(t=cosa+sina=\sqrt{2}cos\left(a-\frac{\eta}{4}\right),t\in\left[-\sqrt{2},\sqrt{2}\right]\)
\(t^2=1+sin2a\Rightarrow sin2a=t^2-1\)
Do đó phương trình trên trở thành:
\(t=1-\frac{1}{2}\left(t^2-1\right)\Leftrightarrow2t=3-t^2\)
\(\Leftrightarrow t^2+2t-3=0\Leftrightarrow t=1,t=-3\)
Vì\(t\in\left[-\sqrt{2},\sqrt{2}\right]\)nên chỉ nhân t=1
\(\Rightarrow cos\left(a-\frac{\eta}{4}\right)=\frac{\sqrt{2}}{2}=cos\frac{\eta}{4}\)
\(\Leftrightarrow a-\frac{\eta}{4}=\pm\frac{\eta}{4}+k2\eta\)
\(\Leftrightarrow a=k2\eta\)hay \(a=\frac{\eta}{2}+k2\eta\)(thỏa điều kiện câu a)
6 tháng 8 2020
2, sin4x+cos5=0 <=> cos5x=cos\(\left(\frac{\pi}{2}+4x\right)\Leftrightarrow\orbr{\begin{cases}x=\frac{\pi}{2}+k2\pi\\x=-\frac{\pi}{18}+\frac{k2\pi}{9}\end{cases}\left(k\inℤ\right)}\)
ta có \(2\pi>0\Leftrightarrow k< >\frac{1}{4}\)do k nguyên nên nghiệm dương nhỏ nhất trong họ nghiệm \(\frac{\pi}{2}\)khi k=0
\(-\frac{\pi}{18}+\frac{k2\pi}{9}>0\Leftrightarrow k>\frac{1}{4}\)do k nguyên nên nghiệm dương nhỏ nhất trong họ nghiệm \(-\frac{\pi}{18}-\frac{k2\pi}{9}\)là \(\frac{\pi}{6}\)khi k=1
vậy nghiệm dương nhỏ nhất của phương trình là \(\frac{\pi}{6}\)
\(\frac{\pi}{2}+k2\pi< 0\Leftrightarrow k< -\frac{1}{4}\)do k nguyên nên nghiệm âm lớn nhất trong họ nghiệm \(\frac{\pi}{2}+k2\pi\)là \(-\frac{3\pi}{2}\)khi k=-1
\(-\frac{\pi}{18}+\frac{k2\pi}{9}< 0\Leftrightarrow k< \frac{1}{4}\)do k nguyên nên nghiệm âm lớn nhất trong họ nghiệm \(-\frac{\pi}{18}+\frac{k2\pi}{9}\)là \(-\frac{\pi}{18}\)khi k=0
vậy nghiệm âm lớn nhất của phương trình là \(-\frac{\pi}{18}\)
LT
3 tháng 4 2017
Đồ thị hàm số y = sin x trên đoạn [-2π, 2π]
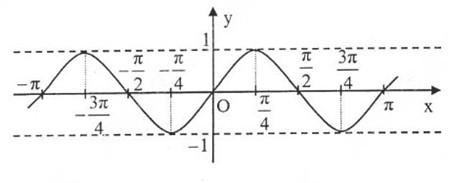
Dựa vào đồ thị hàm số y = sinx
a) Những giá trị của x ∈ [−3π2,2π][−3π2,2π] để hàm số y = sin x nhận giá trị bằng -1 là:
x=−π2;x=3π2x=−π2;x=3π2
b) Những giá trị của x ∈ [−3π2,2π][−3π2,2π] để hàm số y = sin x nhận giá trị âm là:
x ∈ (-π, 0) ∪ (π, 2 π)
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 3 2021
1.
\(\lim\limits_{x\rightarrow0}\dfrac{\sqrt{x+2}-\sqrt{2-x}}{x}=\lim\limits_{x\rightarrow0}\dfrac{2x}{x\left(\sqrt{x+2}+\sqrt{2-x}\right)}=\lim\limits_{x\rightarrow0}\dfrac{2}{\sqrt{x+2}+\sqrt{2-x}}=\dfrac{2}{2\sqrt{2}}=\dfrac{\sqrt{2}}{2}\)
Vậy cần bổ sung \(f\left(0\right)=\dfrac{\sqrt{2}}{2}\) để hàm liên tục tại \(x=0\)
2.
a. \(f\left(0\right)=\lim\limits_{x\rightarrow0^-}f\left(x\right)=\lim\limits_{x\rightarrow0^-}\left(x+\dfrac{3}{2}\right)=\dfrac{3}{2}\)
\(\lim\limits_{x\rightarrow0^+}f\left(x\right)=\lim\limits_{x\rightarrow0^+}\dfrac{\sqrt{x+1}-1}{\sqrt[3]{1+x}-1}=\lim\limits_{x\rightarrow0^+}\dfrac{x\left(\sqrt[3]{\left(x+1\right)^2}+\sqrt[3]{x+1}+1\right)}{x\left(\sqrt[]{x+1}+1\right)}\)
\(=\lim\limits_{x\rightarrow0^+}\dfrac{\sqrt[3]{\left(x+1\right)^2}+\sqrt[3]{x+1}+1}{\sqrt[]{x+1}+1}=\dfrac{3}{2}\)
\(\Rightarrow f\left(0\right)=\lim\limits_{x\rightarrow0^+}f\left(x\right)=\lim\limits_{x\rightarrow0^-}f\left(x\right)\) nên hàm liên tục tại \(x=0\)
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 3 2021
2b.
\(\lim\limits_{x\rightarrow1^-}f\left(x\right)=\lim\limits_{x\rightarrow1^-}\dfrac{x^3-x^2+2x-2}{x-1}=\lim\limits_{x\rightarrow1^-}\dfrac{x^2\left(x-1\right)+2\left(x-1\right)}{x-1}\)
\(=\lim\limits_{x\rightarrow1^-}\dfrac{\left(x^2+2\right)\left(x-1\right)}{x-1}=\lim\limits_{x\rightarrow1^-}\left(x^2+2\right)=3\)
\(\lim\limits_{x\rightarrow1^+}f\left(x\right)=f\left(1\right)=\lim\limits_{x\rightarrow1^+}\left(3x+a\right)=a+3\)
- Nếu \(a=0\Rightarrow f\left(1\right)=\lim\limits_{x\rightarrow1^-}f\left(x\right)=\lim\limits_{x\rightarrow1^+}f\left(x\right)\) hàm liên tục tại \(x=1\)
- Nếu \(a\ne0\Rightarrow\lim\limits_{x\rightarrow1^-}f\left(x\right)\ne\lim\limits_{x\rightarrow1^+}f\left(x\right)\Rightarrow\) hàm không liên tục tại \(x=1\)
MH
9 tháng 4 2017
a) =
=
.
b) =
=
.
c) =
=
.
d) y' =\(\dfrac{\left(x^2+7x+3\right)'\left(x^2-3x\right)-\left(x^2+7x+3\right)\left(x^2-3x\right)'}{\left(x^2-3x\right)^2}\)=\(\dfrac{\left(2x+7\right)\left(x^2-3x\right)-\left(x^2+7x+3\right)\left(2x-3\right)}{\left(x^2-3x\right)^2}\)=\(\dfrac{-2x^2-6x+9}{\left(x^2-3x\right)^2}\)
Lời giải:
TXĐ: $\mathbb{R}\setminus \left\{-1\right\}$
$y=\frac{x^2}{x^3+1}$
$y'=\frac{x(2-x^3)}{(x^3+1)^2}$
$y'=0\Leftrightarrow x=0$ hoặc $x=\sqrt[3]{2}$ (tm TXĐ)
Lập bảng biến thiên với các mốc sau:
$-\infty;-1; 0; \sqrt[3]{2}; +\infty$ thì ta thu được:
Hàm nghịch biến trên $(-\infty; -1)\cup (-1;0)\cup (\sqrt[3]{2}; +\infty)$
Hàm đồng biến trên $(0;\sqrt[3]{2})$
Hàm có giá trị cực tiểu $y_{ct}=y(0)=0$ tại $x=0$
Hàm có giá trị cực đại $y_{cđ}=y(\sqrt[3]{2})=\frac{\sqrt[3]{4}}{3}$ tại $x=\sqrt[3]{2}$