Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi I là tâm đường tròn bàng tiếp góc A của tam giác ABC
Ta có:
SABC=SABI+SACI−SBIC
=Rb/2 + Rc/2 − Ra/ 2
=R. (b+c−a/2)
=R(p−a)
=> R = S/(p-a) (đpcm)

Xét tam giác ABC có I là tâm đường tròn nội tiếp
\(\Rightarrow S_{ABC}=S_{AIB}+S_{BIC}+S_{CIA}=\frac{1}{2}AB.r+\frac{1}{2}BC.r+\frac{1}{2}CA.r\)
\(=\frac{1}{2}\left(AB+BC+CA\right).r=p.r\)
\(\Rightarrow r=\frac{S_{ABC}}{p}\)

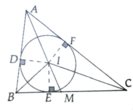
a, Áp dụng tính chất 2 tiếp tuyến tại A,B,C ta chứng minh được b + c - a 2 = AD
b, S A B C = S A I B + S B I C + S C I A
Mà ID = IE = IF = r => S A B C = p.r
c, Vì AM là phân giác của
B
A
C
^
=>
B
M
M
C
=
B
A
A
C
Áp dụng tính chất tỉ lệ thức thu được BM = a c c + b

\(\frac{S}{h_a}+\frac{S}{h_b}+\frac{S}{h_c}=\frac{1}{2}\left(a+b+c\right)=p=\frac{S}{r}\)
\(\Rightarrow\frac{1}{r}=\frac{1}{h_a}+\frac{1}{h_b}+\frac{1}{h_c}\)
Học tốt!!!!!!!!!!!!!!!!