

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Đáp án B.
Phương pháp: Ứng dụng tích phân để tính thể tích khối tròn xoay.
Cách giải: Gắn hệ trục tọa độ Oxy như hình vẽ:
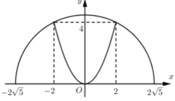
Ta có:
Phương trình đường tròn: ![]()
Phương trình parabol: ![]()
Thể tích khối cầu 
Thể tích khi quay phần tô đậm quanh trục Ox là: 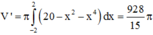
=> Thể tích cần tính 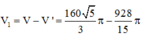
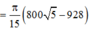

Đáp án A.
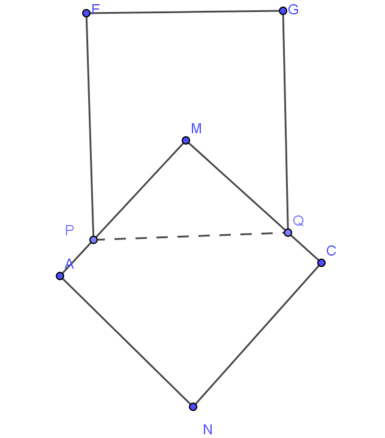
Gọi V 1 là thể tích khối trong xoay khi xoay hình vuông EGQP quanh MN. Khối này có bán kính đáy R = 1 2 E G = 5 2 và đường cao = EP = 5 => V 1 = 5 . 5 2 2 π = 125 4 π
Gọi V 2 là thể tích khối tròn xoay khi xoay hình vuông AMCN quanh MN, khối này là hợp lại của 2 khối nón đêu có bán kính đáy R = 1 2 A C = 5 2 2 Đường cao h = 1 2 M N = 5 2 2 => V 2 = 2 . 1 3 . 5 2 2 . 5 2 2 2 π = 125 2 6 π
Gọi V 3 là thể tích của khối nón tròn xoay khi quay MPQ quanh MN, khối này óc bán kính đáy R = 1 2 P Q = 5 2 đường cao h = d ( M ; P Q ) = 5 2 => V 3 = 1 3 . 5 2 . 5 2 2 . π = 125 12 π
Ta có thể tích của toàn khối tròn xoay V = V 1 + V 2 - V 3 = 125 1 + 2 π 6

Đáp án B
Ta có thể tích vật thể tròn xoay được tạo ra S = S 1 + S 2 .
S 1 = π − 5 2 2 5 25 − x 2 2 d x = 500 π 3 .
S 2 = 1 3 π 5 2 2 3 = π .125.2 2 3.8 = 125 π 2 6
Vậy S = 1000 π + 125 π 2 6 .

Đáp án A
Khi quay quanh AB, hình vuông ABCD sinh ra mặt trụ có thể tích V 1 = πa 3
Hình thang AMCB sinh ra hình nón cụt có thể tích
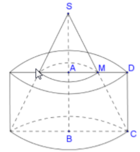

Quay miền tam giác SAB quanh cạnh SA ta được khối nón có chiều cao h = SA , bán kính đáy R = A B .
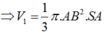
Quay nửa hình tròn quanh cạnh SA ta được khối cầu có bán kính IA.
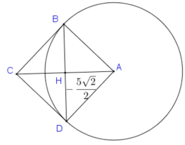
Áp dụng tính chất đường phân giác ta có:
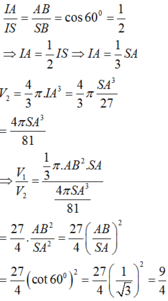
Chọn D.