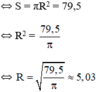Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) (Bài đọc thêm SGK trình bày cho các bạn cách sử dụng máy tính CASIO fx-220. Tuy nhiên hiện nay loại máy tính này không còn phổ biến, vậy nên bài làm dưới đây VietJack sẽ trình bày theo cách sử dụng các dòng máy tính CASIO fx – 570 và VINACAL).
+ Nhập hàm số: 
+ Nhập giá trị:

Vậy ta có bảng sau:
| R (cm) | 0,57 | 1,37 | 2,15 | 4,09 |
| S = πR2 | 1,02 | 5,9 | 14,52 | 52,55 |
b) Gọi bán kính mới là R’. Ta có R’ = 3R.
Diện tích mới là :
S ' = π R ' 2 = π ( 3 R ) 2 = π 9 R 2 = 9 π R 2 = 9 S
Vậy khi bán kính tăng lên 3 lần thì diện tích tăng 9 lần.
c) Diện tích hình tròn bằng 79,5
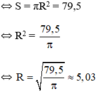

Bạn chịu khó gõ đề chay (viết nguyên chữ thôi, những chỗ cần công thức thì mở hộp $\sum$, không chèn hình, không chèn ký hiệu khác ngoài) để bài dễ nhìn hơn, nâng cao khả năng hỗ trợ giải bài.
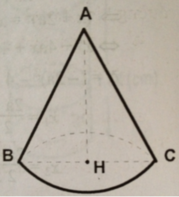
Bài như này nhìn rất "khó chịu" (hình minh họa bên dưới)

a, Tính được r = 1,44cm Þ Smc = 4p r 2 = 26,03 c m 2
b, Ta có V c = 4 3 πR 2 = 15 , 8 cm 3 => R = 1,56cm
=> V h n = 1 3 πR 2 h ≈ 2 , 53 πcm 3

Diện tích xung quanh hình trụ bằng 314 c m 2
⇔ 2.π.r.h = 314
Mà r = h
⇒ 2 π r 2 = 31 ⇒ r 2 ≈ 50
⇒ r ≈ 7,07 (cm)
Thể tích hình trụ: V = π ⋅ r 2 h = π ⋅ r 3 ≈ 1109 , 65 cm 3
Kiến thức áp dụng
Hình trụ có bán kính đáy r, chiều cao h thì:
+ Diện tích xung quanh: Sxq = 2πrh
+ Thể tích: V = π.r2.h

Diện tích xung quanh hình trụ bằng 314cm2
⇔ 2.π.r.h = 314
Mà r = h
⇒ 2πr2 = 314
⇒ r2 ≈ 50
⇒ r ≈ 7,07 (cm)
Thể tích hình trụ: V = π.r2.h = π.r3 ≈ 1109,65 (cm3).

Áp dụng BĐT sau:\(2\left(a^2+b^2\right)\ge\left(a+b\right)^2\) ( dùng BĐT Bunhiacopski mà chứng minh :D )
Ta có:\(\frac{a+b}{a^2+b^2}=\frac{41}{9}\Rightarrow\frac{a^2+b^2}{a+b}=\frac{41}{9}\)
\(\Rightarrow\frac{82}{9}=\frac{2\left(a^2+b^2\right)}{a+b}\ge\frac{\left(a+b\right)^2}{a+b}=a+b\)
\(\Rightarrow a+b\le9\)
Mặt khác:\(41\left(a+b\right)=9\left(a^2+b^2\right);\left(41;9\right)=1\Rightarrow a+b⋮9\Rightarrow a+b=9\)
\(\Rightarrow a^2+b^2=41\)
Ta có hệ:\(\hept{\begin{cases}a+b=9\\a^2+b^2=41\end{cases}}\) giải cái hệ này là ra a,b nha < 3