Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn C
Xét hàm số f(x) = | x 2 + a x + b |. Theo đề bài, M là giá trị lớn nhất của hàm số trên [-1;3]
Suy ra
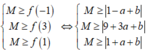
Nếu M = 2 thì điều kiện cần là 
và 
cùng dấu
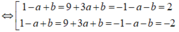
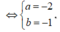
Ngược lại, khi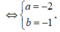 
Ta có, hàm số 
M là giá trị lớn nhất của hàm số f(x) trên [-1;3] 
Vậy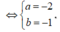 
Ta có: a + 2b = -4.
Chọn C
Ta có 
. Dấu 
xảy ra khi 
.
Ta có 
. Dấu 
xảy ra khi 
.
Xét hàm số 
, có 
.
Trường hợp 1: 
. Khi đó 
.
Áp dụng bất đẳng thức 
ta có 
.
Trường hợp 2:
. Khi đó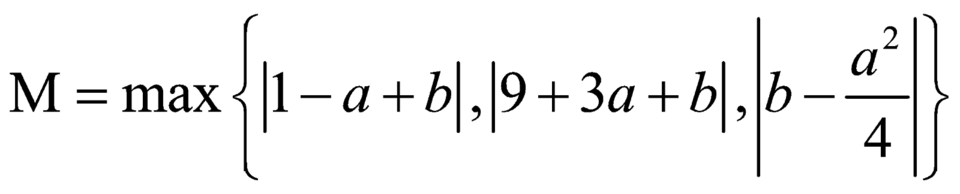 
.
Áp dụng bất đẳng thức 
và
ta có 
.
Suy ra 
.
Vậy 
nhận giá trị nhỏ nhất có thể được là 
khi 
.
Do đó 
.
\(f'\left(x\right)=3x^2-6x=0\Rightarrow\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)
\(f\left(-1\right)=-2;f\left(0\right)=2;f\left(2\right)=-2\)
\(\Rightarrow M=2;m=-2\Rightarrow P=6\)
Cả 4 đáp án đều sai (kiểm tra lại đề bài, có đúng là \(f\left(x\right)=x^3-3x^2+2\) hay không?)
Ta có
Từ (1) và (2), kết hợp với x + y + z ≥ x + y + z ta được
Giá trị nhỏ nhất của M là 2 .
Dấu bằng xảy ra khi
cùng dấu
Do đó a = - 2 b = - 1 ⇒ a b = 2
Chọn A.
\(g\left(x\right)=x^4-4x^3+4x^2+a\)
\(g'\left(x\right)=4x^3-12x^2+8x=0\Leftrightarrow4x\left(x^2-3x+2\right)\Rightarrow\left[{}\begin{matrix}x=0\\x=1\\x=2\end{matrix}\right.\)
\(f\left(0\right)=f\left(2\right)=\left|a\right|\) ; \(f\left(1\right)=\left|a+1\right|\)
TH1: \(\left\{{}\begin{matrix}M=\left|a\right|\\m=\left|a+1\right|\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}\left|a\right|\ge\left|a+1\right|\\\left|a\right|\le2\left|a+1\right|\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}-\dfrac{2}{3}\le a\le-\dfrac{1}{2}\\a\le-2\end{matrix}\right.\) \(\Rightarrow a=\left\{-3;-2\right\}\)
TH2: \(\left\{{}\begin{matrix}M=\left|a+1\right|\\m=\left|a\right|\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}\left|a+1\right|\ge\left|a\right|\\\left|a+1\right|\le2\left|a\right|\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}-\dfrac{1}{2}\le a\le-\dfrac{1}{3}\\a\ge1\end{matrix}\right.\) \(\Rightarrow a=\left\{1;2;3\right\}\)
Đáp án D
Phương pháp:
Dựa vào đồ thị hàm số ta xác định được điểm cao nhất và điểm thấp nhất của đồ thị trên đoạn [-1;3]
Tung độ điểm cao nhất là giá trị lớn nhất của hàm số, tung độ điểm thấp nhất là giá trị nhỏ nhất của hàm số trên đoạn [-1;3].
Từ đó ta tìm được: M;m => M-m
Cách giải:
Từ đồ thị hàm số ta thấy trên đoạn [-1;3] thì điểm cao nhất của đồ thị là điểm A(3;3) và điểm thấp nhất của đồ thị là B(2;-2) nên GTLN của hàm số là M=3 và GTNN của hàm số là m = -2
Từ đó M - m = 3 - (-2) = 5
Chọn B
Ta có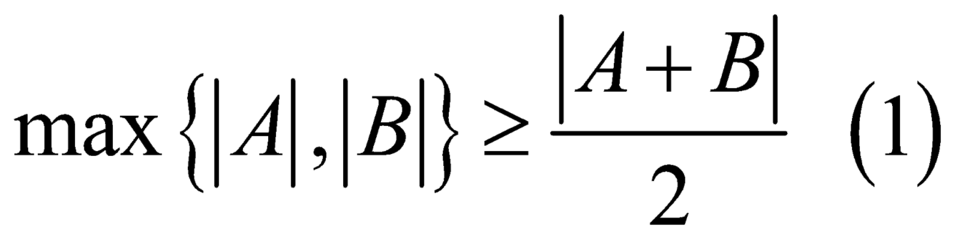
.
Dấu = xảy ra khi A=B.
Ta có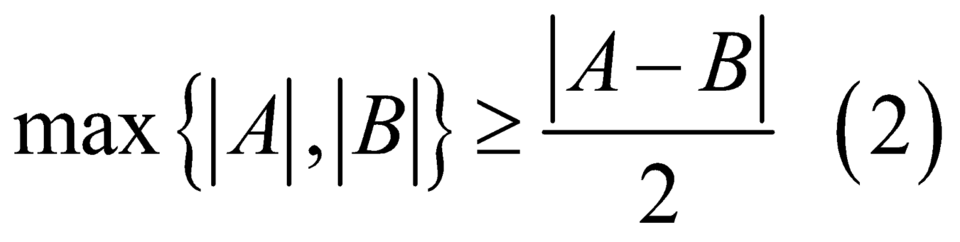
.
Dấu = xảy ra khi A= -B.
Xét hàm s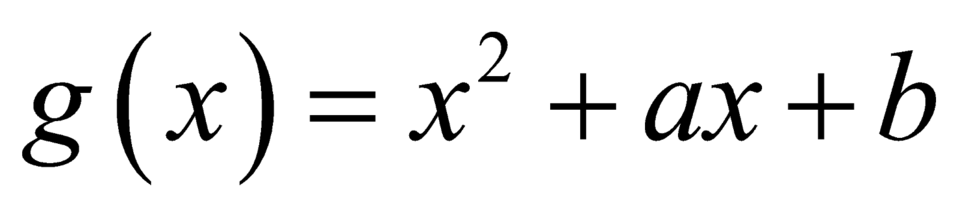ố
, có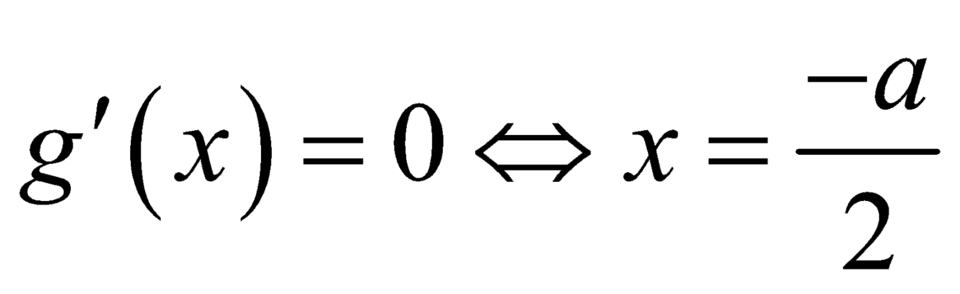 
.
Trường hợp 1: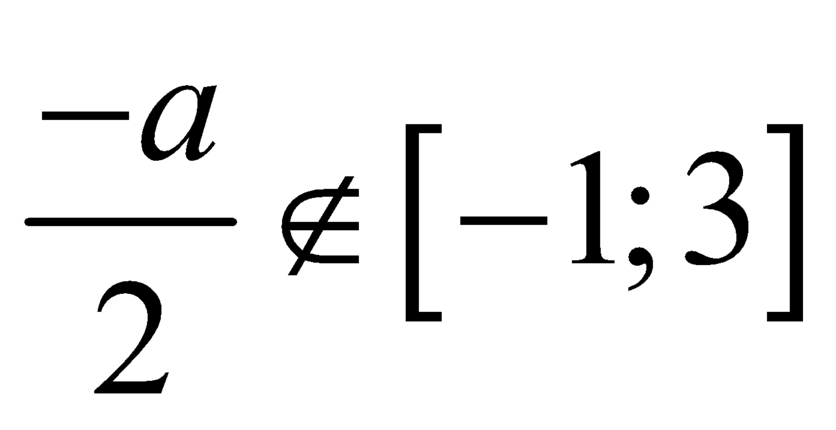
.
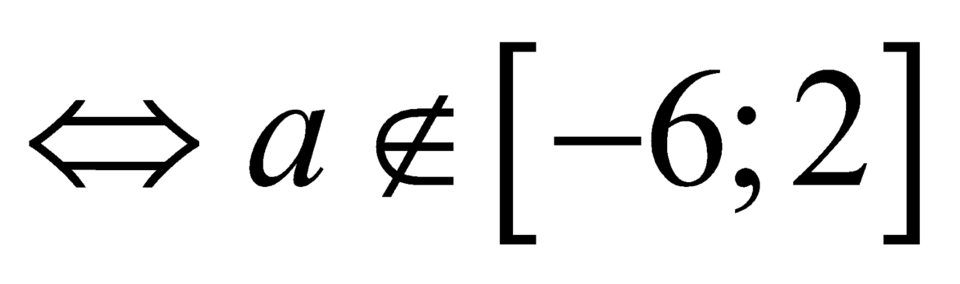Khi đó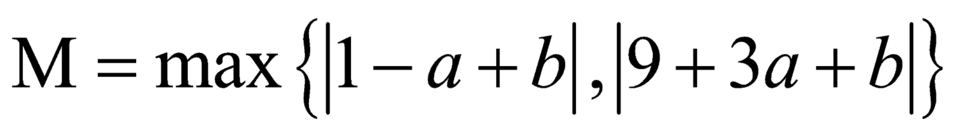
.
Áp dụng bất đẳng thức (1) ta có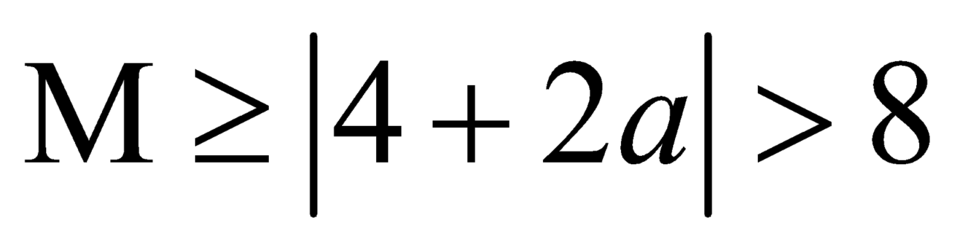
.
Trường hợp 2: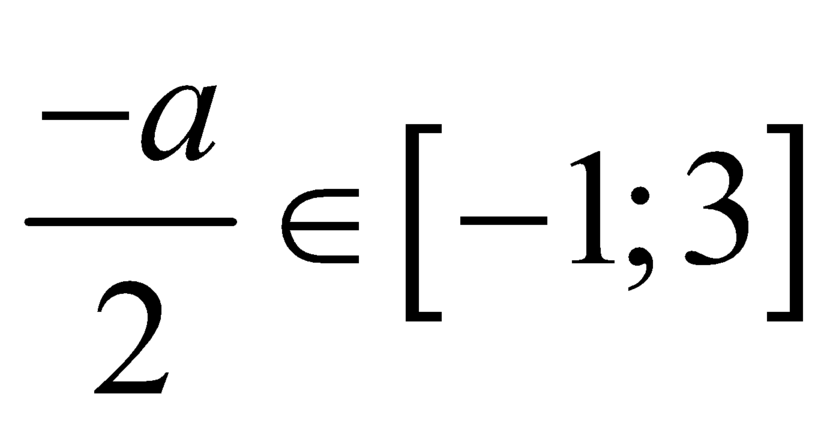
.
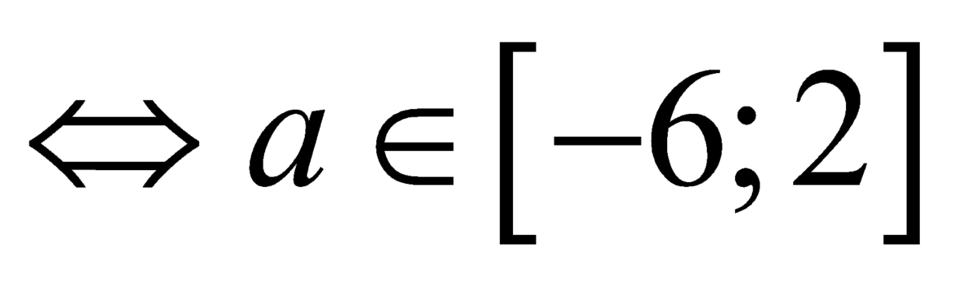Khi đó
.
Áp dụng bất đẳng thức (1) và(2) ta có
Suy ra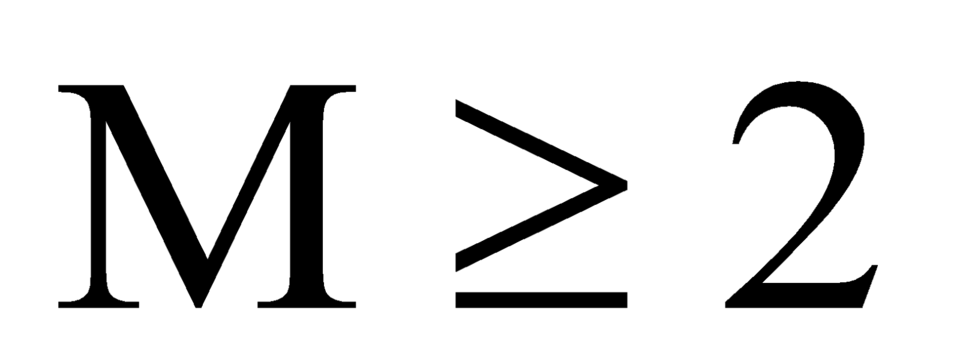
.
Vậy M nhận giá trị nhỏ nhất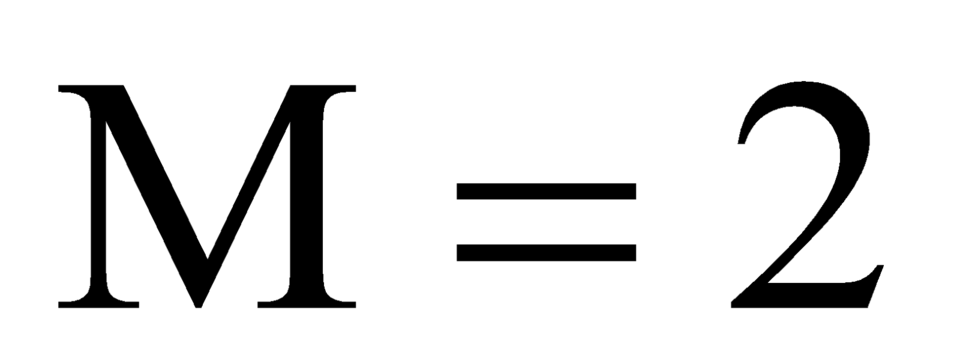
khi
Do đó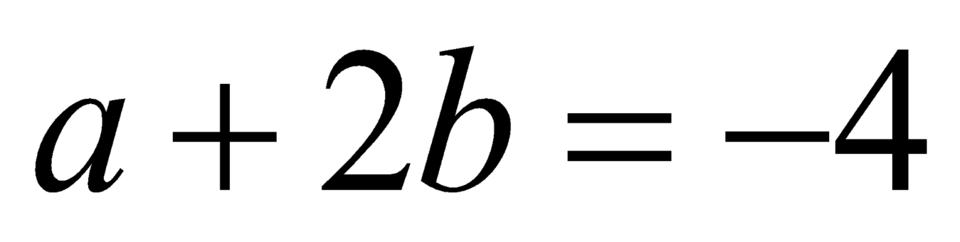
.