Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi x (h) (x > 0) là khoảng thời gian chuyển động của ôtô đi từ A đến C.
Ô tô đi với vận tốc 48km/h ⇒ Quãng đường AC bằng: 48.x (km) (1)
Vì xe máy đi trước ôtô 1 giờ nên thời gian xe máy đi từ A đến C bằng: x + 1 (h)
Xe máy đi với vận tốc 32km/h ⇒ Quãng đường AC bằng: 32(x + 1) (km) (2)
Từ (1) và (2) ta có phương trình: 48x = 32(x + 1).
Vậy phương trình là: 48x = 32(x + 1).

| Vận tốc (km/h) | Quãng đường đi (km) | Thời gian đi (h) | |
| Xe máy | 35 | s | 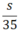 |
| Ô tô | 45 | 90 – s | 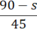 |
Ô tô xuất phát sau xe máy 2/5 giờ nên
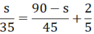

Gọi x là thời gian chuyển động của ô tô (x > 0; giờ)
Đoạn đường của ô tô đi trong x giờ: 48 x
Đoạn đường của xe máy đi trong x giờ: 32x
Vì xe máy khởi hành trước ô tô là 1 giờ nên khi hai xe cùng khởi hành thì đã cách nhau 32 km.
Ta có phương trình cần tìm:
48x – 32 x = 32

Quãng đường HN đến Đồ Sơn là 100 + 20 = 120 km
Thời gian ô tô từ HN đến Đồ Sơn là: 120 : 60 = 2 (giờ)
Ô tô thứ hai đi từ Hải phòng về HN cũng phải mất 2 giờ => Vận tốc ô tô thứ hai là: 100 : 2 = 50 (km/h)
Ô tô thứ hai đi 45' (tức là 0,75 giờ) là: 50 x 0,75 = 37,5 (km)
Quãng đường còn lại ô tô thứ hai còn phải đi là: 100 - 37,5 = 62,5 (km)
Ô tô thứ hai sửa mất 30' (tức 0,5 giờ) => Để đến HN như thời gian dự kiến (tức tổng thời gian 2 giờ), thì thời gian ô tô thứ hai đi trong quãng đường còn lại là: 2 - 0,75 - 0,5 = 0,75 (giờ)
=> Vận tốc ô tô thứ hai phải đi trong quãng đường còn lại (62,5 km) là:
62,5 : 0,75 = 250/3 (km/h) (gần = 83,333 km/h)
Sau khi ô tô thứ hai sửa xong, ô tô thứ nhất đã đi được: 60 x (0,75+ 0,5) = 75 km
Ta thấy 75km lớn hơn quãng đường từ HN đến chỗ xe thứ hai hỏng (62,5). Vậy 2 xe gặp nhau chỗ ô tô thứ hai hỏng và cách HN 62,5 km.
Lúc đó thời gian ô tô thứ nhất đi là: 62,5 : 60 = 62,5/60 giờ = 62,5 phút
Lúc gặp nhau là: 8h + 62,5' = 9h2,5'
ĐS: ....

Do xe máy khởi hành trước ô tô 1 giờ nên khi ô tô và xe máy gặp nhau sau x giờ kể từ khi ô tô khởi hành thì thời gian xe máy đi được đến lúc gặp nhau là: x + 1 (giờ)
Quãng đường ô tô đi được là 48x (km)
Quãng đường xe máy đi được là: 32(x+1) (km)
Mà hai quãng đường trên bằng nhau nên ta có phương trình:
48x = 32(x+1)
Vậy phương trình biểu thị việc ô tô gặp xe máy sau x giờ, kể từ khi ô tô khởi hành là: 48x = 32(x+1)
k cho mk nha
Gọi x (h) (x > 0) là khoảng thời gian chuyển động của ôtô từ khi khởi hành cho đến khi gặp xe máy.
Vì xe máy đi trước ôtô 1 giờ nên thời gian chuyển động của xe máy là: (x + 1) (h).
Đoạn đường của ôtô đi trong x giờ: 48x (km).
Đoạn đường của xe máy đi trong (x + 1) (h): 32(x + 1) (km).
Ô tô gặp xe máy khi hai quãng đường bằng nhau:
48x = 32(x + 1)
Vậy phương trình là: 48x = 32(x + 1)

| v(km/h) | t(h) | s(km) | |
Xe máy | 32 | x + 1 | 32(x+1) |
| Ô tô | 48 | x | 48x |
Giải
Sau x giờ quãng đường ô tô đi đc là
(48x( km) )
Xe máy khởi hành trước ô tô 1(h) nên thời diêm 2 xe gặp nhau ,xe máy đã đi trong ( x+1) ( h)
Quãng đường xe máy đi được tới lúc 2 xe gặp nhau là
32(x +1) ( km)
ta có phương trình biểu thị ô tô gặp xe máy
48x= 32(x+1)
Trong x giờ, ôtô đi được 48x (km)
Xe máy đi trước ôtô 1 giờ nên thời gian xe máy đi là x + 1 (giờ)
Ôtô và xe máy đi cùng chiều và gặp nhau nên quãng đường hai xe đi được là bằng nhau.
Vậy phương trình cần tìm là:
32(x + 1) = 48x
Trong x +1 (giờ) xe máy đi được 32(x + 1)(km)
Chúc bạn học Tốt!!!!^-^!!!!
Giải theo cách chọn ẩn của Tròn:
Gọi thời gian từ lúc xe máy khởi hành đến lúc hai xe gặp nhau là: x (giờ) (x > 0)
Đổi 20 phút = \(\frac{{20}}{{60}} = \frac{1}{3}\) (giờ)
Thời gian ô tô xuất phát từ Hải Phòng đi Hà Nội đến lúc hai xe gặp nhau là: \(x - \frac{1}{3}\) (giờ)
Vì xe máy đi với vận tốc 40 km/h, ô tô đi với vận tốc 60km/h, quãng đường Hà Nội đến hải Phòng là 120km nên ta có phương trình:
\(40{\rm{x}} + 60.\left( {x - \frac{1}{3}} \right) = 120\)
Ta có:
\(\begin{array}{l}40{\rm{x}} + 60.\left( {x - \frac{1}{3}} \right) = 120\\40{\rm{x}} + 60{\rm{x}} - 20 = 120\\100{\rm{x}} = 140\\x = \frac{{140}}{{100}} = \frac{7}{5}\end{array}\)
Đổi \(\frac{7}{5}\) giờ = 1 giờ 24 phút
Sau 1 giờ 24 phút , kể từ lúc xe máy khời hành thì hai xe gặp nhau.
Giải theo cách chọn ẩn của Vuông:
Gọi quãng đường từ Hà Nội đến điểm gặp nhau của hai xe là x(km)
Quàng đường từ Hải Phòng đến điểm hai xe gặp nhau là 120 – x (km)
Thời gian xe máy đi từ Hà Nội đến điểm hai xe gặp nhau là: \(\frac{x}{{40}}\)(giờ)
Thời gian ô tô đi từ Hải Phòng đến điểm hai xe gặp nhau là: \(\frac{{120 - x}}{{60}}\)(giờ)
Đổi 20 phút = \(\frac{{20}}{{60}} = \frac{1}{3}\) (giờ)
Vì ô tô đi sau xe máy 20 phút nên ta có phương trình:
\(\frac{x}{{40}} = \frac{{120 - x}}{{60}} + \frac{1}{3}\)
Ta có:
\(\begin{array}{l}\frac{x}{{40}} = \frac{{120 - x}}{{60}} + \frac{1}{3}\\\frac{{3{\rm{x}}}}{{120}} = \frac{{240 - 2{\rm{x}}}}{{120}} + \frac{{40}}{{120}}\\3{\rm{x}} = 240 - 2{\rm{x + }}40\\3{\rm{x}} + 2{\rm{x}} = 280\\5{\rm{x}} = 280\\x = 280:5\\x = 56\end{array}\)
Thời gian xe máy đi từ Hà Nội đến điểm hai xe gặp nhau là: \(\frac{{56}}{{40}} = \frac{7}{5}\)(giờ)
Đổi \(\frac{7}{5}\) giờ = 1 giờ 24 phút
Sau 1 giờ 24 phút , kể từ lúc xe máy khời hành thì hai xe gặp nhau.
Vậy giải theo cách chon ẩn của bạn Tròn thì cách giải sẽ ngắn gọn hơn.