K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
LT
1
BT
25 tháng 10 2015
Bạn Sáng nói bạn ấy chỉ mới học lớp 6 mà giải được? Đồ coi theo, đồ copy...Tui xem thường..##@@
HH
4
CM
19 tháng 6 2017
Lời giải của bạn Hà sai, lời giải của bạn Quang đúng.
Vì 5x4 chia hết cho 2x2;
–4x3 chia hết cho 2x2;
6x2y chia hết cho 2x2
Do đó A = 5x4 – 4x3 + 6x2y chia hết cho 2x2 hay A chia hết cho B.
Chú ý: Đơn thức A chia hết cho đơn thức B nếu tìm được đơn thức Q sao cho A=B.Q
Ví dụ : Cho hai đơn thức A= 2x2y3; B = 7xy
Khi đó với đơn thức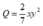 
thì A=B.Q
Do đó, đơn thức A chia hết cho đơn thức B.
PT
1
CM
24 tháng 11 2019
Do đó A = 15x4 - 8x3 + x2 chia hết cho 
hay A chia hết cho B.
b) A = x2 - 2x + 1 = (x – 1)2
Vậy A chia hết cho x – 1 hay A chia hết cho B.
CM
2 tháng 8 2019
Hạng tử y 6 của đa thức A không chia hết cho đơn thức B = 2x.
Do đó, đa thức A không chia hết cho đơn thức B
Chọn đáp án A